Reglas de reemplazo o equivalencia
No siempre un argumento valido o invalido se puede comprobar por medio de las reglas de inferencia; por eso, se utilizan otras reglas conocidas como reglas de reemplazo o reglas de equivalencia, que sustituyen o reemplazan (segun sea necesario) para lograr la demostración o prueba de validez del argumento.
Equivalencia material (EM)
Permite reescribir la bicondicional.
Exportación (EXP)
Permite cambiar de conjunción a condicional y viceversa, modificando su agrupación.
Transposición (TRAN)
Permite conmutar las variables lógicas de la condicional negando cada una de estas.
Implicación material (IMP)
Permite cambiar de disyunción a condicional y viceversa.
Asociación (ASO)
Permite agrupar diferentes formas de las variables lógicas, siempre y cuando sea el mismo operador
Tautología (TAU)
Permite unir dos variables lógicas en una sola.
Distribución (DIS)
Permite distribuir la variable lógica de afuera y su operador lógico con las variables lógicas de dentro y su operador lógico.
Doble negación (DN)
Si la negación de cualquier proposición p verdadera es falsa, entonces cuando se vuelve a negar esta sera nuevamente verdadera y viceversa.
Conmutación(CONM)
Permite cambiar el orden de las variables lógicas sin cambiar el operador lógico.
Leyes de De Morgan (DM)
Permite cambiar de disyunción a conjunción y viceversa, negando ambas variables logicas.
REFERENCIA BIBLIOGRAFICA
Recuperado de https://elibro.net/es/ereader/biblioibero/39454?page=30
Villalpando Becerra, J. F. (2015). Matemáticas discretas: aplicaciones y ejercicios. México: Grupo Editorial Patria.
PRESENTADO POR:
SANDRA MILENA RODRÍGUEZ CASTILLO
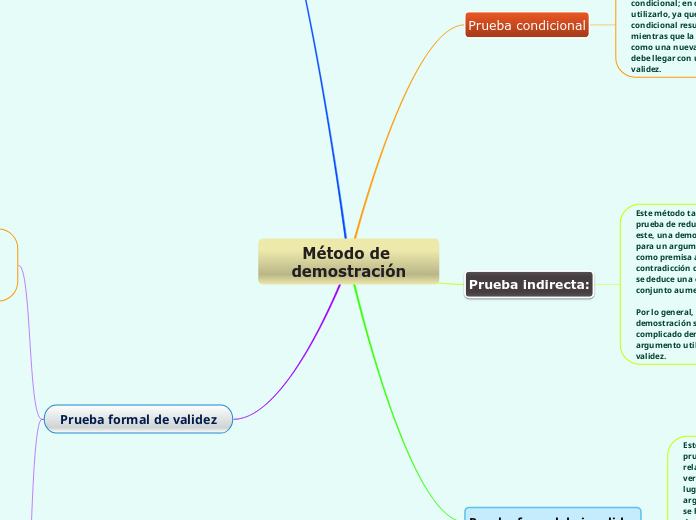
Método de demostración
Prueba formal de invalidez
Este metodo también se conoce como prueba por asignación de valores. Esta muy relacionado con el metodo de tablas de verdad, la diferencia consiste en que en lugar de construir la tabla de verdad para el argumento, la demostración de la invalidez se hace de tal modo que se asignan valores de verdad a las proposiciones simples, de modo que las premisas sean verdaderas y la conclusión falsa; es decir, se dan valores a la con- clusión tal que su resultado sea falso y luego se trata de utilizar esos valores de verdad en los antecedentes, junto con la combinación de estos, segun sea la conveniencia.
Para obtener la invalidez de un argumento por el metodo de la prueba de invalidez se efectúan los siguientes pasos:
1. Asignar variables proposicionales a cada proposición simple.
2. Obtener la traducción lógica de las premisas.
3. Organizar el argumento de forma horizontal, uniendo las premisas con el operador lógico /\.
4. Asignar valores de verdad a la conclusión, de tal manera que esta resulte falsa.
5. Tomando en cuenta los valores de verdad asignados a la conclusión, hacer que las premisas del argumento sean verdaderas, resolviendo las operaciones lógicas indicadas. El símbolo de por tanto (5.) equivale a la condicional :>
Prueba indirecta:
Este método también se conoce corno prueba de reducción al absurdo. Mediante este, una demostración indirecta de validez para un argumento dado se construye como premisa adicional a la negación o la contradicción de su conclusión, con lo que se deduce una contradicción explícita del conjunto aumentado de las premisas.
Por lo general, este metodo de demostración se utiliza cuando resulta complicado demostrar la validez de un argumento utilizando la prueba formal de validez.
Para demostrar la validez de un argumento por el metodo de prueba indirecta, se deben seguir los si- guientes pasos:
1. Asignar variables proposicionales a cada proposición simple.
2. Obtener la traducción lógica de las premisas.
3. Organizar el argumento con sus premisas en forma vertical, escribiendo antes de cada premisa un numero de premisa consecutivo.
4. Negar la conclusión escribiendo a su derecha Pl, para indicar que la premisa es obtenida por prueba indirecta, e incluirla como una premisa mas.
5. Del conjunto total de premisas, empleando las leyes lógicas, deducir una contradicción. El proceso de inferencia concluye cuando se llega a dicha contradicción.
Prueba condicional
Este método se aplica solo a argumentos que tengan como conclusión una condicional; en otros casos no sería posible utilizarlo, ya que el antecedente de la condicional resulta ser una premisa mas, mientras que la conclusión se determina como una nueva conclusión a la cual se debe llegar con una prueba formal de validez.
Para demostrar la validez de un argumento por el método de la prueba condicional se deben seguir los siguientes pasos:
1. Asignar variables proposicionales a cada proposición simple.
2. Obtener la traducción lógica de las premisas.
3. Organizar el argumento con sus premisas en forma vertical, escribiendo antes de cada premisa un numero de premisa consecutivo.
4. El antecedente de la conclusión se convierte en una premisa mas, escribiendo a su derecha PC, para indicar que la premisa obtenida es por prueba condicional, y se deja el consecuente como la conclusión.
5. Utilizar el procedimiento de la prueba formal de validez tomando en cuenta la nueva conclusión.
El proceso de inferencia concluye cuando se llega a la nueva conclusión del argumento.
Prueba formal de validez
Pasos para demostrar la validez de un argumento.
La prueba formal de validez consiste en deducir la conclusión del argumento en función de sus premisas, esto es, que las premisas infieran la conclusión. A fin de que una demostración, por la prueba formal de validez, resulte perfectamente clara, se deben seguir los siguientes pasos:
1, Asignar variables proposicionales a cada proposición simple.
2. Realizar la traducción lógica de las premisas.
3. Organizar el argumento con sus premisas en forma vertical, escribiendo antes de cada premisa un numero de premisa consecutivo.
4. Utilizar las reglas de inferencia y/o de reemplazo que conduzcan a nuevas premisas (inferencias). Estas siempre deben ser antecedidas por un nuevo número de premisa. Al utilizar las reglas se debe escribir su abreviatura y el número o números de las premisas de las que se ha deducido.
5. El proceso de inferencia termina cuando se llega a la conclusión del argumento.
Ademas del proceso anterior, tambien es necesario considerar algunas condiciones para la demostración:
1. Utilizar todas las premisas.
2. Utilizar todas las nuevas premisas obtenidas.
3. Es posible utilizar las premisas las veces que sean necesarias.
Cuando el argumento tiene mas de tres proposiciones simples diferentes no es facil determinar la validez o invalidez de un argumento mediante tablas de verdad, pues resultaría bastante tedioso hacer dicha tabla de verdad, ademas de que se puede incurrir en errores involuntarios.
Por ese motivo, el método mas conveniente para obtener la validez de los argumentos es la prueba formal de validez, la cual utiliza reglas validas, como las reglas de inferencia y las reglas de reemplazo o equivalencia. Pero, antes de utilizar las reglas de inferencia y las reglas de reemplazo o equivalencia, primero es necesario conocer su definición y sus aspectos fundamentales.
Pero, antes de utilizar las reglas de inferencia y las reglas de reemplazo o equivalencia, primero es nece- sario conocer su definición y sus aspectos fundamentales.
Reglas de inferencial
Las reglas de inferencia son formas de argumentos cuya validez puede ser demostrada por tablas de verdad; ademas, estas reglas permiten establecer conclusiones muy bien formadas y validas a partir de otras premi- sas. En general son usadas para analizar los argumentos con muchas premisas o cuando se tienen cuatro o mas proposiciones simples.
Dilema constructivo (DC)
Permite eliminar los antecedentes de las dos condicionales, dando como resultado la disyunción de los consecuentes.
Conjunción (CONJ)
Permite unir dos premisas diferentes.
Simplificación (SIM)
Permite eliminar las variables proposicionales que no se necesiten.
Adición (AD)
Permite agregar las variables proposicionales que se necesiten.
Silogismo hipotético (SH)
Permite eliminar el consecuente de la primera premisa y el antecedente de la segunda premisa, siempre y cuando sean iguales.
Silogismo disyuntiva (SD)
Permite eliminar una de las dos disyunciones siempre que una de las dos este negada en la segunda premisa.
Modus tollens (MT)
Permite eliminar el consecuente siempre y cuando esté negado en la segunda premisa, dando como consecuencia el antecedente negado.
Modus ponens (MP)
Permite eliminar el antecedente siempre que la segunda premisa sea dicho antecedente.
Metodo de tabla de verdad
Una tabla de verdad, o tabla de valores de verdad, es una tabla que rnuestra el valor de verdad de una proposición cornpuesta, así corno de algunos casos de proposiciones sirnples, cuando estas utilizan los operadores lógicos de negación y doble negación, dependiendo de los operadores lógicos usados y de los valores de verdad de las proposiciones sirnples involucradas.
La importancia de las tablas de verdad radica en que gran parte del razonamiento lógico y de las relaciones entre proposiciones se pueden ilustrar a traves de estas.
Para construir una tabla de verdad se efectúan los siguientes pasos:
1. Asignar variables proposicionales a cada proposición simple.
2. Obtener la traducción lógica de la proposición compuesta.
3. Obtener la cantidad de todas las combinaciones de valores de verdad de las premisas. La cantidad de valores de verdad esta dado por la fórmula 2 a la n, donde n es la cantidad de variables proposicionales de las premisas.
Clasificación de argumentos: tautología, contradicción y contingencia.
A partir del resultado de las tablas de verdad, es posible clasificar los argumentos en tres tipos: tautología, contradicciones y contingencias.
Cuando un argumento es una tautología se considera que este es valido, pero si es una contradicción es inválido; lo mismo ocurre con una contingencia. Para obtener la validez de un argumento por tabla de verdad se efectúan los siguientes pasos:
1. Asignar variables proposicionales a cada proposición simple.
2. Obtener la traducción lógica de las premisas.
3. Organizar el argumento en forma horizontal, uniendo las premisas con el operador lógico /\.
4. Obtener la cantidad de todas las combinaciones de valores de verdad de las premisas. La cantidad de valores de verdad esta dado por la fórmula 2 ala n, donde n es la cantidad de variables proposicionales de las premisas.
Una tautología es una proposición que es verdadera para todos los posibles valores de verdad de sus componentes simples.
Una proposición es llamada contradicción o absurdo si ofrece un resultado falso para todos los posibles valores de verdad de sus componentes simples.
Una proposición es una contingencia cuando puede ser verdadera o falsa, dependiendo de los valores de verdad de sus componentes simples.