a Mario Leonardo Calero Ramón 4 éve
976
Organigrama
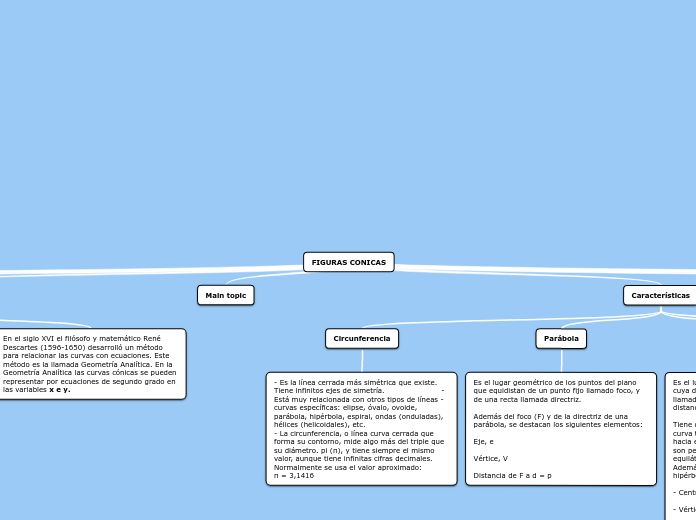
Una parábola se define como el conjunto de puntos en un plano que equidistan de un punto fijo llamado foco y una línea recta denominada directriz. El eje focal es perpendicular a la directriz y pasa por el foco, actuando como el eje de simetría de la parábola.