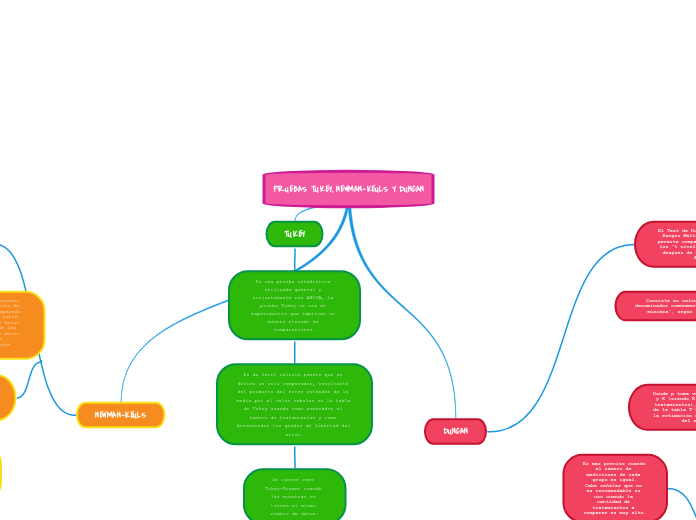
PRUEBAS TUKEY, NEWMAN-KEULS Y DUNCAN
DUNCAN
El Test de Duncan o Prueba de Rangos Múltiples de Duncan permite comparar las medias de los “t niveles” de un factor después de haber utilizado ANOVA.
Consiste en calcular varios "rangos", denominados comúnmente “rangos significativos mínimos”, según la siguiente fórmula:
D p = da k - glerror (raíz cuadrada) de CMerror / n
Donde p toma valores entre 2 y K (siendo K el número de tratamientos), d se obtiene de la tabla T-9 y CMerror es la estimación de la varianza del error.
Este Test permite comparar tratamientos no relacionados, es decir, todos los tratamientos contra todos, a fin de establecer un orden de méritos.
Es más preciso cuando el número de mediciones de cada grupo es igual.
Cabe señalar que no es recomendable su uso cuando la cantidad de tratamientos a comparar es muy alto.
Alda Pascuzzo-Lima. . (2019). Test de Duncan. 26 de abril, de Análisis Estadísticos para Ensayos Clínicos y Estudios Epidemiológicos. Asesoría estadística para investigación, en general, incluyendo Tesis. Asesoría Metodológica. Diseño de Posters para Congresos y Eventos Científicos. Sitio web: http://aldanalisis.blogspot.com/2019/04/test-de-duncan.html
TUKEY
Es una prueba estadística utilizada general y conjuntamente con ANOVA, La prueba Tukey se usa en experimentos que implican un número elevado de comparaciones.
Es de fácil cálculo puesto que se define un solo comparador, resultante del producto del error estándar de la media por el valor tabular en la tabla de Tukey usando como numerador el número de tratamientos y como denominador los grados de libertad del error.
Se conoce como Tukey-Kramer cuando las muestras no tienen el mismo número de datos.
Dado que el análisis de varianza acuse un efecto significativo, la prueba de Tukey provee un nivel de significancia global de α cuando los tamaños de las muestras son iguales y de α a lo sumo a cuando no son iguales.
Se basa en la construcción de intervalos de confianza de las diferencias por pares. Si estos intervalos incluyen al 0, entonces no se rechaza la hipótesis nula.
https://www.scientific-european-federation-osteopaths.org/wp-content/uploads/2019/01/PRUEBAS-POST-HOC.pdf
NEWMAN-KEULS
Permite comparar las medias de los t niveles de un factor después de haber rechazado la Hipótesis nula de igualdad de medias mediante la técnica ANOVA.
Todos los procedimientos involucran el cálculo de un valor que es comparado con la diferencia entre promedios. Si este valor es más pequeño que las diferencias quiere decir que éstas son significativamente diferentes.
Este Test utiliza un umbral móvil basado en el número de medias que están implicadas en el recorrido de la resta de medias comparada sin que el nivel de significación cambie, se altere, es decir, se mantiene en el general, que suele ser 0.05.
Esto le convierte en un Test más conservador.
Tradicionalmente, las comparaciones múltiples se realizan al mismo nivel de significancia que el ANOVA. Por ejemplo, para un ANOVA significativo a un nivel de 5% (a = 0,05), se realizan comparaciones múltiples al 5%.
Alda Pascuzzo-Lima. . (2015). Pruebas de Comparación Múltiple: Test de Newman-Keuls. 7 de julio, de Análisis Estadísticos para Ensayos Clínicos y Estudios Epidemiológicos. Asesoría estadística para investigación, en general, incluyendo Tesis. Asesoría Metodológica. Diseño de Posters para Congresos y Eventos Científicos. Sitio web: http://aldanalisis.blogspot.com/2015/07/pruebas-de-comparacion-multiple-test-de.html