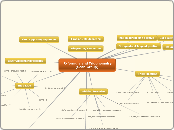
R-formula and Trigonometry(Sean Group)
The text covers various fundamental concepts and formulas in trigonometry, presenting a comprehensive overview of trigonometric ratios, identities, and the R-formula. It starts by detailing specific angle values for sine, cosine, and tangent functions, and then introduces key addition and subtraction formulas for trigonometric functions.
Megnyitás
R-formula and Trigonometry(Sean Group) R-formula Tan alpha = b/a Where R=Square root of Asquare + b Square acosx+bsinx=Rcos(x-a)/ acosx-bsinx=Rcos(x+a) asinx+bcosx=R sin(x+a)/ asinx-bcosx= Rsin(x-a) Double angle formulae tan2A=2tanA/1-tansquare A cos2A=cos square A- sin square A/ 2cos square A- 1/ 1-2sin square A sin2A=2sinAcosA Addition formulae cos(a-b)=cosacosb+sinasinb tan(a-b)=tana-tanb/1+tanatanb tan(a+b)=tana+tanb/1-tanatanb cos(a+b)=cosacosb-sinasinb sin(a-b)=sinacosb-cosasinb sin(a+b)=sinacosb+cosasinb trigo ratio tan60=square root 3 tan45=1 tan30=1/squareroot 3 cos60=1/2 cos45=1/squareroot2 cos30=squareroot 3 /2 sin60=squareroot 3 /2 sin45=1/square root 2 sin30=1/2 Trigo identites sin square x+ cos sqaure x=1 1+tan square= sec square cosecx=1/sinX 1+cot square = cosec square secx=1/cosx Cotx=1/tanx Tanx= Opposite/adjacent 4th quadrant cosine positive 3rd quadrant tangent positive 2nd quadrant sine positive 1st quadrant all positive 1degree=π/180degree 1 radian=180degree/π Cosx=Adjacent/hypotenus Sinx=Opposite/Hypotenus
