a Mileidy Gonzalez Gonzalez 3 éve
1138
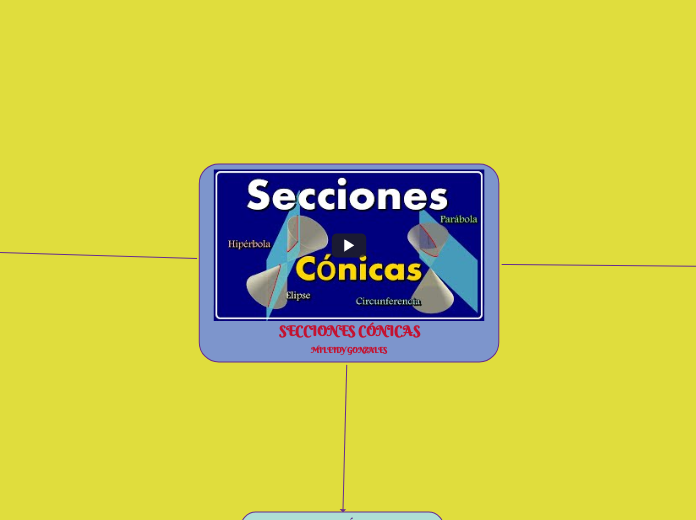
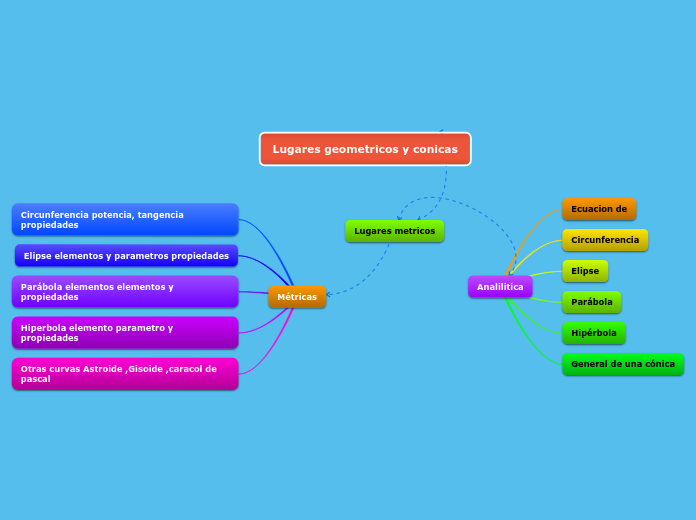
SECCIONES CÓNICAS MILEIDY GONZALEZ
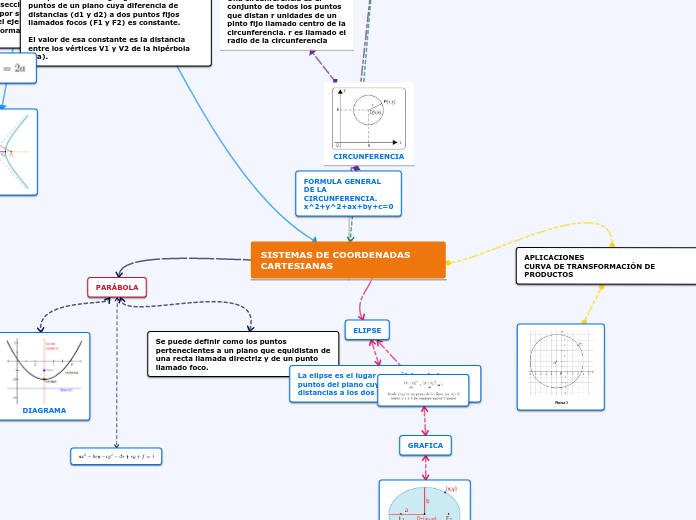
Las secciones cónicas son figuras geométricas obtenidas al cortar un cono con un plano en diferentes ángulos y posiciones. Estas secciones incluyen la parábola, la circunferencia, la elipse y la hipérbola, cada una con propiedades y elementos característicos.