a fernando chaves 8 éve
385
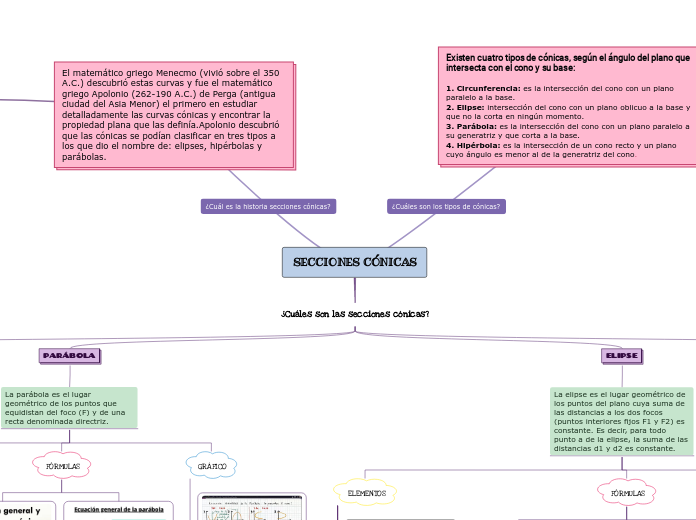
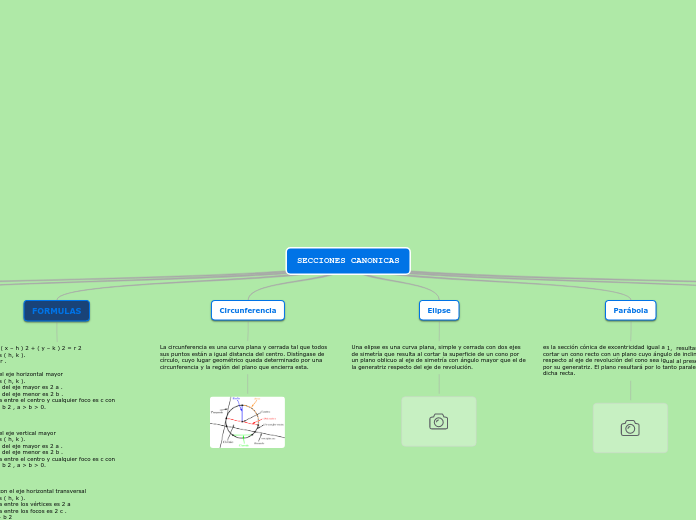
SECIONES CONICAS
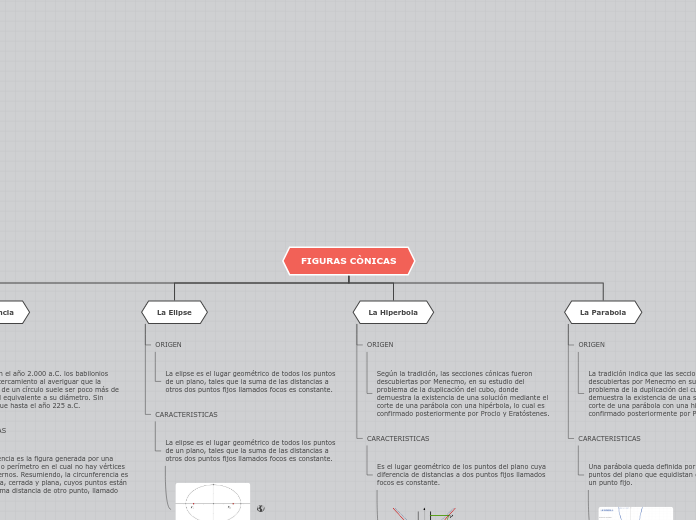
Las secciones cónicas son curvas que resultan de la intersección de un cono con un plano y se dividen en cuatro tipos principales: elipse, parábola, hipérbola y circunferencia. Cada tipo de cónica se define por sus propiedades geométricas y ecuaciones específicas.