El matemático alemán George Cantor (1845-1918) demostró en el siglo XIX que el infinito de los reales es más grande que el infinito de los naturales. Y no demostró sólo eso, también probó que el infinito de los irracionales es mayor que el de los racionales. Y que el de los racionales es igual al de los naturales, aun cuando los primeros son densos y los naturales no lo son. En otras palabras, Cantor mostró que los racionales son contables, es decir, están en relación biunívoca con los naturales. Los reales, por otro lado, no son contables, y los irracionales tampoco.
Una de las definiciones de número racional dice que todos los números racionales tienen una expresión decimal finita, o periódica. Esto quiere decir que si en vez de escribirlo como fracción lo escribimos como un entero con decimales (por ejemplo 12.44386),
En matemáticas, a esto se le conoce como correspondencia biunívoca.
SOBRE LOS NÚMEROS, NATURALES, REALES, IMAGINARIOS.
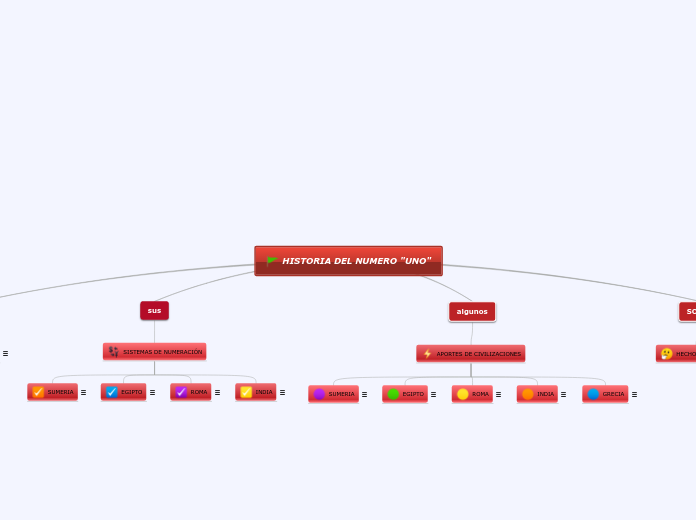
La primera etapa de la numeración: se estableció una correspondencia uno a uno entre un grupo de objetos y otro, o incluso entre un conjunto de objetos y un conjunto de abstracciones o ideas.
En matemáticas y en cualquier área del conocimiento que se preocupe por contar y medir, se ocupan los números.
Números Reales
Definimos los reales ℝ como el conjunto que contiene a los racionales y a los irracionales. Como ℝ contiene a ℚ, es fácil ver que los reales son densos. Pero no sólo eso, ahora podemos decir que la recta real (la representación de ℝ en la recta) es continua. Es decir, a diferencia de como pasaba con los racionales, la recta real no tiene huecos. No resulta sorprendente, pues así fueron construidos: que sean completos es uno de sus axiomas. Los matemáticos decimos entonces que los reales son un espacio completo, y esta es la razón por la cual la mayor parte de la geometría se construye en el plano real.
se necesitan en todo tipo de cálculos que van desde la medicina hasta la astrofísica
Son los más usados en la ciencia.
Racionales
Imaginemos una recta horizontal, como aquella con la que nos enseñaron a sumar en la primaria, con la ranita que saltaba. En medio se encontraba el cero y de cada lado iban apareciendo líneas con números: a la derecha empezaba el 1, luego el 2, y se seguía con los demás naturales manteniendo siempre la misma distancia entre cada uno de ellos. A la izquierda del cero iban apareciendo los enteros negativos, como si reflejáramos a los naturales en el cero.
Una de las razones por la cual los racionales son tan importantes es que son densos. ¿Qué significa esto? Imaginemos que tenemos dos números racionales cualesquiera, q y r. Si nos encontráramos trabajando únicamente con números enteros podría suceder que no existiera un número entre ellos. Es decir un número c mayor que q pero menor que r. Por ejemplo, no existe ningún entero entre el 7 y el 8. Pero este no es el caso de los racionales porque entre un número racional y otro siempre existe otro número racional, seleccionen el que seleccionen. Basta con sumarlos y dividir el resultado entre dos. De hecho, no sólo hay un número entre ellos: hay una infinidad de números racionales entre dos de ellos. Esto se vuelve claro si pensamos que podemos repetir el proceso de sumar y dividir entre dos cuantas veces queramos, siempre encontrando un número mayor que el primero y menor que el segundo.
Números Naturales
Son aquellos que surgen directamente del proceso de contar. Uno, dos, tres, cuatro…un millón…etc. En el mundo de las matemáticas se les define de manera breve como: ℕ= {1, 2, 3, …}*
Básicamente lo que hay que hacer es seguir tres pasos. Primero, se prueba que aplica para el elemento más chico del conjunto. Luego, se hace la suposición de que el n-ésimo elemento (es decir, un elemento arbitrario n) también cumple con la propiedad. Entonces, si con esto se logra probar que el elemento n + 1 tiene esa propiedad podemos concluir que todo el conjunto la tiene
Podemos ver inmediatamente es que el más pequeño de todos es el número 1
Si elijo cualquier número natural, puedo encontrar el siguiente que sea mayor al elegido: lo único que tengo que hacer es sumarle 1.