a Leonardo Delgado 4 éve
1380
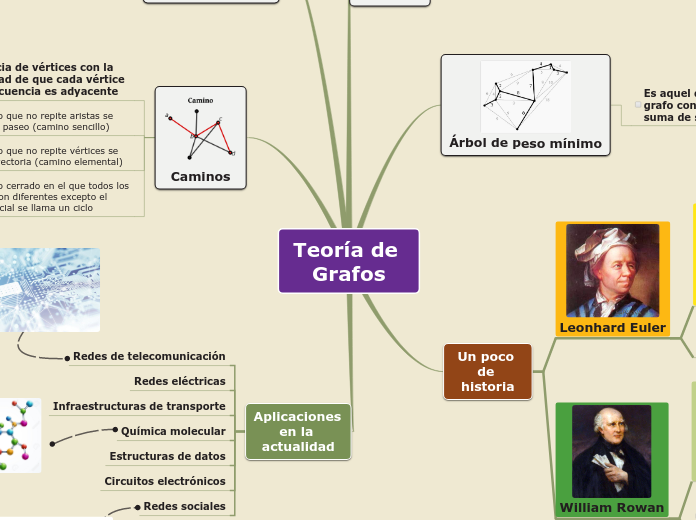
Teoría de Grafos
Graph theory encompasses various concepts such as paths, cycles, and trees, each with distinct characteristics and definitions. Paths are sequences of vertices connected by edges, with cycles being closed paths where the initial and final vertices are the same, excluding other repetitions.
Megnyitás
La Topología Se convirtió en lo que se conoce como topología algebraica Estrechamente relacionada con la teoría de grafos Teoría de Grafos Aplicaciones en la actualidad Redes sociales Circuitos electrónicos Estructuras de datos Química molecular Infraestructuras de transporte Redes eléctricas Redes de telecomunicación Caminos Un camino cerrado en el que todos los vértices son diferentes excepto el vértice inicial se llama un ciclo Un camino que no repite vértices se llama trayectoria (camino elemental) Un camino que no repite aristas se denomina paseo (camino sencillo) Secuencia de vértices con la propiedad de que cada vértice de la secuencia es adyacente Grafos Conjunto de objetos llamados nodos o vértices, que pueden estar conectados por líneas llamada aristas. Un poco de historia William Rowan Inventó un rompecabezas que involucraba encontrar un camino en un dodecaedro que pasa por cada esquina una vez Circuito Hamiltoniano Leonhard Euler Resolvió el problema de encontrar un camino sin cruzar ningún puente dos veces Puente de Königsberg Árbol de peso mínimo Es aquel que obtenemos en un grafo conexo y sin ciclos, la suma de sus aristas es mínima Árboles Es una gráfica conexa que no contiene ciclos
