da Francy Espitia mancano 3 anni
439
SECCIONES CÒNICAS
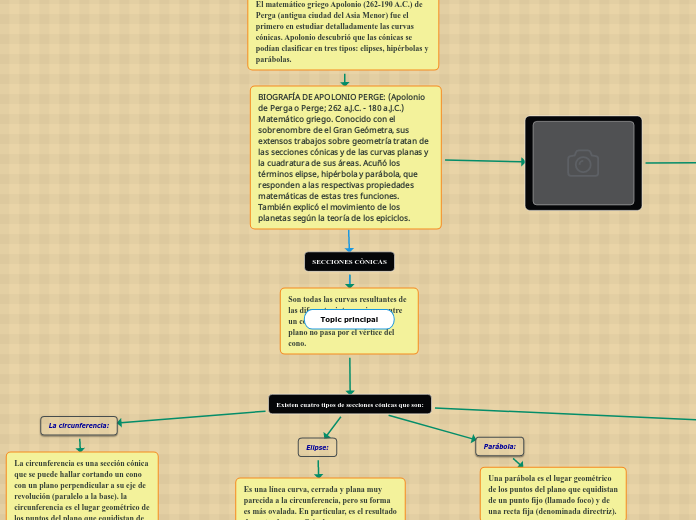
Las secciones cónicas son figuras geométricas que se obtienen al cortar un cono con un plano, y se clasifican en cuatro tipos principales: elipse, hipérbola, parábola y circunferencia.
da Francy Espitia mancano 3 anni
439

Più simili a questo
ASIGNATURAS: TECNOLOGÍA Y MATEMÁTICAS
GRADO: 1102
AÑO: 2021
Se consigue una hipérbola cuando se corta un cono mediante un plano con un ángulo menor. Una hipérbola se puede definir como el lugar geométrico de los puntos del plano que cumplen la siguiente propiedad: el valor absoluto de la diferencia de las distancias desde un punto cualquiera de la hipérbola hasta dos puntos fijos (llamados focos) debe ser constante.
Una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo (llamado foco) y de una recta fija (denominada directriz).
Es una línea curva, cerrada y plana muy parecida a la circunferencia, pero su forma es más ovalada. En particular, es el resultado de cortar la superficie de un cono con un plano oblicuo. La elipse es la curva plana y cerrada, cuya suma de distancias desde cada punto hacia dos puntos F1 y F2 es constante. Los puntos F1 y F2 se denominanan los focos de la elipse.
La circunferencia es una sección cónica que se puede hallar cortando un cono con un plano perpendicular a su eje de revolución (paralelo a la base). la circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.