da omar brito mancano 2 anni
251
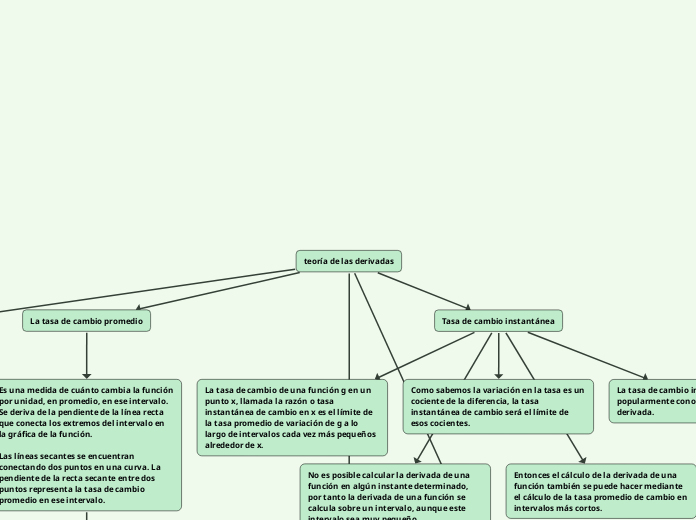
teoría de las derivadas
La teoría de las derivadas se centra en medir la rapidez con la que cambia una función en un punto específico. Para entender este concepto, se utiliza la tasa de cambio promedio que se obtiene de la pendiente de una línea secante que conecta dos puntos de una curva.