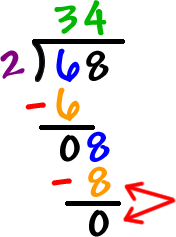Scientific Notation
Orderof Operations
Parenthesis Exponent Multiplication Division Addition Subtraction
*There are four levels in order of operation Groups of number, exponents, division/multiplication, subtraction/addition*
G
E
M D
A S
Fractions (Mixed Numbers)
Back wards C
Multiply the whole number and denominator and then add the product to the numerator.


You can also show the fractions as indicated above and in the modeling subtopic .
10/2- What is it?
- How many times 2 goes into 10 evenly
-Total number divided by # of groups= # in each (FULL) group
KCF ( Keep Change Flip)
1.)When dividing numbers you need to change the sign to multiplication and flip the fraction.
*Also if you have a mixed fraction you need to turn it in an improper fraction before continuing*
2.) Find the ones before cross multiplying
3.) Cross multiply
*if you successfully found the ones then your answer is in the simplfied form *


Modeling
*Note: If you have an example as 1/3(1/2) to find the answer you do the rectangles and shade them in as we did in last week's lesson.The box that has two colors shadedin is the numeritor.*
Find the ones
Find the ones is an alterntaive way for students to simplify the fractions before multiplying. You are able to simply them as a fraction and acrosso from one another
Example: 22/5 *65/11
2/1*13/1= 26
Fractions (Unlike Dem)
Subtraction
Examples
*This rule for subtraction and addition can be applied in basic mathematics along with upper mathematics such as algebra*
Basic Math:
Problem: 3/5+1/6
Find LCM: (6/6)3/5+(5/5)1/6
Add: 18/30+5/30=23/30
Problem:18- 4/7
Find LCM: 17 7/7- 4/7
Subtraction: 17 3/7
Problem: 27+4/9
Addition: 27 4/9
Algebra:
Example:
3/5x+ 1/6x
(6/6) 3/5x+ (5/5) 1/6x
18/30x+ 5/30x= 23/30x
Example:
7/(x+3) + 2/(x+5)
(x+5/x+5) 7/(x+3) + (x+3)/(x+3) 2/(x+5)
7x+35/x^2+8x+15 + 2x+6/x^2+8x+15
= 9x+41/x^2+8x+15
Addition
1.)We need to find the LCM/LCD of the fractions. An easier way to find them is to write the factors that equal the number below it.
1/6 + 1/4
2*3 2*2
2.)After, multiply the fraction with the number that isn't the same
(2/2) 1/6+ (3/3) 1/4
3.)This equals=
2/12+3/12=5/12
*This rule applies when subtraction with unlike denominators. The goal is to find the same denominator*
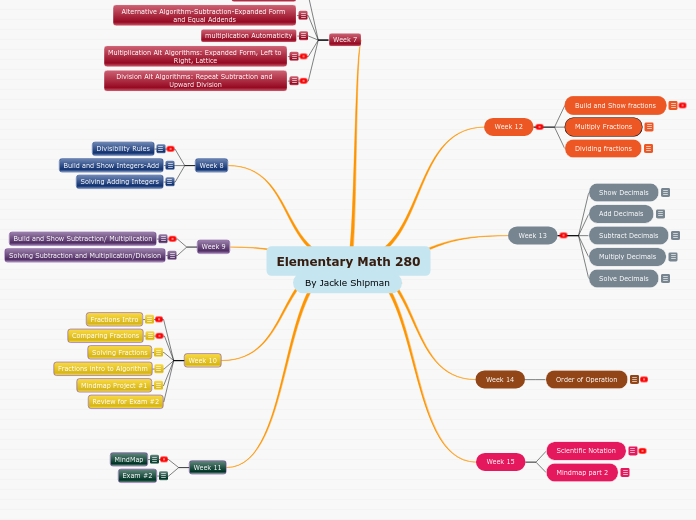
Week 13-14
Importance
Why do we need to find common denominators when we add/subtract fractions, but not when we multiply/divide?
Makes it easier to easier if they have same numbers
Fractions
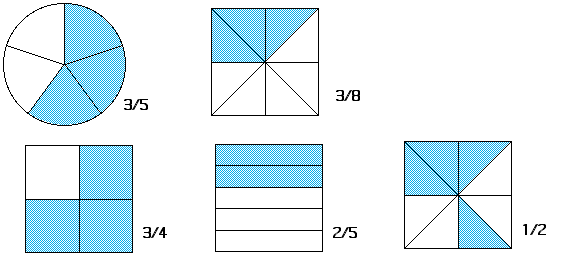
Simplifying
Simplifying Fractions: fraction is in the simplest form when the top and bottom cannot be any smaller.
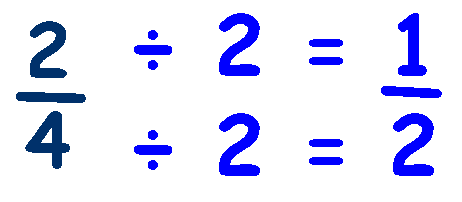
Equivalent
Equivalent Fractions: have same value although they look different.
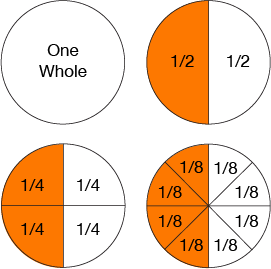
Week 11-12
Fractions w/Models
Set Model
Set Model: Using individual shapes to match fractions
Can use: Two colored counters
Cubes
Foam Shapes
Etc.
*create a "1" fraction such as 2/2 or 9/9*
_d.jpg)
Linear
Linear Model: Lenght of whole is divided into equal lengths

Area Model: show a visual representationof the product of two fractions. Helps with multpliying and reducing.
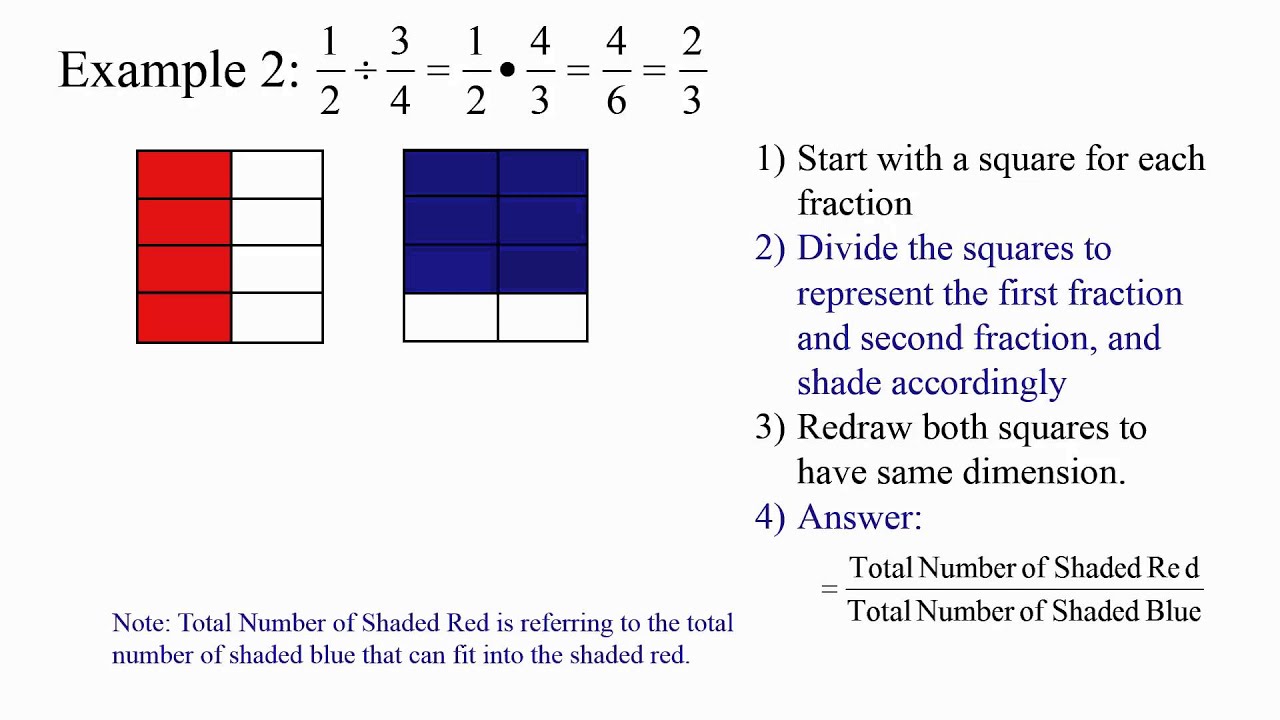
Multiplication Cont.
Factoring Polynomiels
Factoring Rule: Be careful where the sign is placed; it goes with the digit

Difference of Square
*be careful of where the sign goes in the box*
*A B C terms: used to describe the numbers of the problem*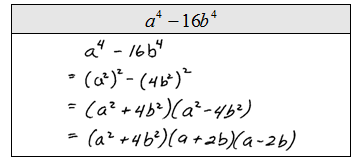
Rational Numbers: numbers you can write as a ratio (fraction)
ex. 3, 4.12
Irrational Numbers: numbers that cannot be written as ratios (fractions)
Note: when a number is being squared (inside the house) and is negative it has no solution as it leads to imaginary numbers
Note: x^2=5
5= +/-5
Scientific Notation/ Standard Form
Definition
Scientific Notation: number that is bigger or equal to one. It is also multilpied by the power of ten.
Standard Form: numbers that are written in standard form
Example: 300, 1, 0.17, 45
Conversion
Multiplying binomials
Number Lines

Distance of Square Formula
Distance Formula

Generic Rectangle

Properties
Properties: makes doing problems easier
Associative: order doesn't change who you "associate" with change
(Parenthesis Exponent Multiplication Division Addition Subtraction)
ex. (4+2)+5 -5+(5+3)
4+ (2+5) (-5+5)+3
Commutative: the order can change
*doesn't work for subtraction*
ex. 5+7
7+5
Distributive: multiplication
*multiplying 2 numbers means finding area*
*multplying 3 numbers means finding volume*

Rules for Multiplication and Division
+ and + is +
+ and - is -
- and - is +
- and + is -
Rules: when signs are the same it's positive. When signs are different it's negative.
*same rules as multiplication apply in division*
*When doing a problem if the coefficent is negative, use a zero bank*

*if the number is bigger than 10 don't show. if it is less thant 10 draw out*
Weeks 8-9
Weeks 4-7
Integers
Integers: All whole positive and negative numbers
Zero-Pairs: A positive and negative number (usually 1) that cancel each other out to make zero.
Zero-Bank: Grouped zero-pairs
Keep Change Change: used for subtraction
Absolute Value: measurement of distance away from zero
Example. |-3|=3
Example. -|-5|=-5 *The sign in front of the absolute value says "the opposite off"
Adding/subtracting
Adding Integers
Drawing: Use if the number is less than 10. Note: Use norms when drawing out the problem. Keep all positive on top in a line and all negative on the bottom and in a line as well.
Ex. 2 add -4
++
- - - -
Diagram: Use if the number is more than 10. Ex. -15 add 436
Step 1. Place the negative or positive on the top of the numbers. You add two signs to the number that will create the longer row and one sign that will create the shorter row.
- ++
-15 +436
Step 2. Circle one sign of each number. If the signs in the circle are a positive and negative you subtract and if the signs are two negatives or two positives you use addition.
- sub.++
-15+ 436
Step 3. After you add or subtract, bring down the sign that is left over since that will determine if the number is positive or negative.
436-15=+421
Number Line
*Note: Some problems will need zero pair/bank to solve.*
Example: -4-1=-5
(Color Key: orange is zero bank, red is eliminated, black is answer)
+++++
- - - - - - - - -
Subtracting Integers
Keep Change Change
Example. -39-(-156)= +117
Step 1. -39+(-156)
Step 2. -39+(+156)
Step 3. -39+156
Step 4. Do regular steps that you would do for diagram
GCF/LCM
Keywords
Greatest Common Factor/ Divisor: Finding the greatest factor that are in common with both number sets. Note: GCF are the smaller numbers.
Factors: numbers that multiply equally to each other. Example the GCf of 2 and 3 is 6.
Least Common Multiple/ Denominator: a common multiple of is a number that is a multiple of the set of numbers given. Note: LCM are the bigger numbers.
Multiples: number that can be divided equally without a remainder. Example 6 is a multiple of 2 and 3.
Prime Numbers: a number that is greater than 1 and the only two factors are 1 and itself. The number 2 is the only even number that is prime.
Composite Numbers: numbers that can be divided evenly by numbers that are not only 1 and itself.
Divisibility Rules
Divisible by:
By 4: Look at the last two digits
By 8: Look at the last three digits
By 5: Look at the numbers ending in 5 or 0
By 10: Numbers ending in 0
By 3: Add numerals= needs to add up as a number to be divided by three
By 6: If number is divisible by 2 and 3 then its divisible by 6
By 9: If number is divisible by 3 then it's divisible by 9
Prime Factorization Methods
*Important Note: To find the GCF/GCD you use the common numbers and use the smallest exponent to multiple them.*
*Note: To find the LCM/LCD you use all the factors that have the biggest exponent and they do not have to be common numbers*
Factor Trees: you stop factoring once a all the numbers are prime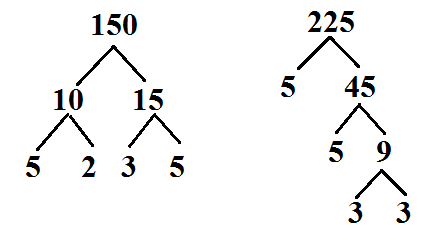
Upwards Division: All the numbers on the side have to be prime

Venn Diagram and Double Bubble: Places all equal numbers in the middle and the different numbers for each set on a different side. 
Alternative Alg.
Division
Long Division: traditional division
*note:to help a student that is having trouble setting up the format of a problem from this 68/2 tell them to create house. When they have trouble with what number to put outside and inside tell them the first number goes IN and the the second number goes OUT. In-&-Out!*
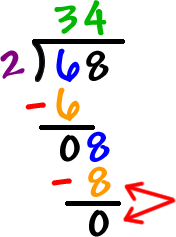
Repeated Subtraction: see YouTube link
Upwards Division: you format the problem like a fraction. You place the first number on top and the second number at the bottom.
*Note: Upwards division helps students with making fractions from the remainder*
Multiplication
Area Model: Create blocks and use the area of each to add to get the entire area.

Lattice Form:
Same format as the addition lattice form. Only difference is multiplying the numbers instead of adding them.

Expanded Form: Expansion of numbers
27x31
(20+7)x(30+1)
Adding Bases
Example
(23 base five) + (21 base five)= 134 units
4 longs 3 units 4 longs 1 unit
|||| ... + |||| .
1 flat 3 longs 4 units
weeks 1-3
Adding using Alt. Alg.
Adding Algorithms- The best method for children to learn about the value of ones and tenth are as follows:
1. Expanded Sum
2. Partial Sums
3. Left to Right
4. Lattice Addition
5. Traditional
Examples:
Traditional Algorithms
24+15=39
Partial Sums (Left to Right)
24+20=34
34+5= 39
Expanded Sum
20+4
+10+5
---------
30+9=39
Lattice Addition(helps with knowing where to place the tenth value)
24
+39
-------
|0/3|0/9|
-----------
39
Multiple Numbers
-Scratch Method
- Compatible Numbers "Friendly Numbers" (estimation)
Groups of tens to add easier
-Front-End Estimation (start to learn how to round)
Example:
31+24+15+42+39 30+20+10+40+39=130
-"Friendly Numbers" Compatible Numbers
Subtracting using Alt. Alg.
Alternatives
Traditional
47-12=35
Partial Difference
47-10=37
37-2= 35
Left to Right
40+7
-(10+2)
----------
30+5= 35
Equal Addition (we want to make the number in the zero state so it is easier to subtract)
47+8 55
-12+8 -20
-----
35
Area Model for Multiple
Area
Example
A rectangle with 4 longs and 4 units.
Length * Height
__ 4(10+1)
__ 40+4
__ 44
__
....
Converting Others to Base Ten
Example:
Convert 23four to base ten
Step 1: Separate them to longs and units
23 four
2 longs 3 Units
Step 2: Multiply the number of longs with the base given
2(4) 3(1)
Step 3: Add the values given after multiplying
8+3= 11
Step 4: Answer is the value after addition
11 Units
Converting Base ten to Others
Notes
Conjecture: Ones values will always be less than base?
False
Example: 6 base to four
| .. = 1 long 2 units= 12 four
*Must always add units even if a number is not presented*
Example: 15 to base five
||| = 3 longs 0 units= 30 five
*You can never have your numbers (units, longs,flats, etc.) be bigger than your base*
Vocabulary
UnDevCarLo
UnDevCarLo
Understand the problem
Develop a plan
Carry out plan
Look back at work
Bases
-Units
-Longs
-Flats
-Cube
-Manipluations
Addition/Subtracting Alg
-Lattice Addition
-Partial Sum
-Left to Right
-Expanded Sum
-Partial Difference
-Equal Addition
-Traditional Algorithms
-Scratch Method
-Compatible Numbers- "Friendly Numbers" (estimation)
-Front end Estimation
-Friendly Numbers (compatible numbers)






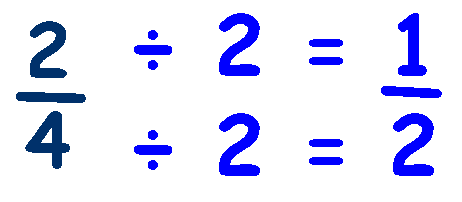
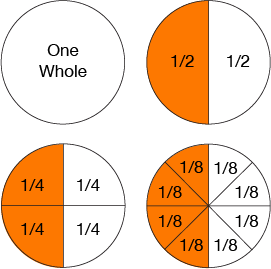
_d.jpg)