によって hector stiven buitrago cardenas 2年前.
125
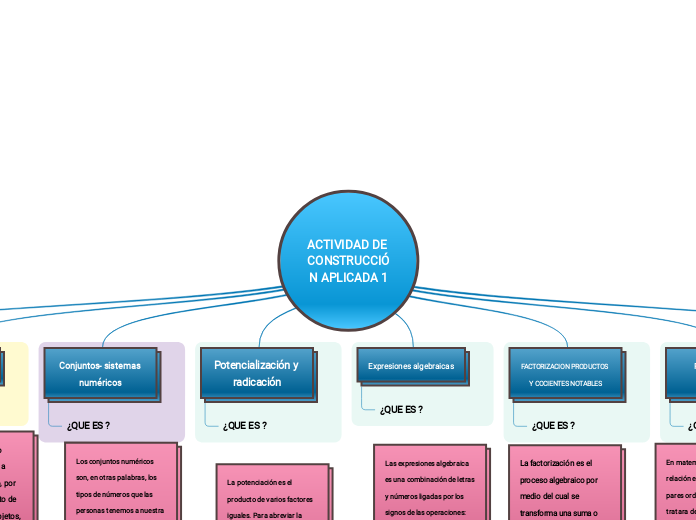
ACTIVIDAD DE CONSTRUCCIÓN APLICADA 1
Los conjuntos numéricos son las distintas clases de números que utilizamos para llevar a cabo operaciones, ya sea en contextos cotidianos o más avanzados. Estos sistemas permiten el conteo y la construcción de todos los números válidos dentro del sistema.