ALGEBRA RELACIONAL
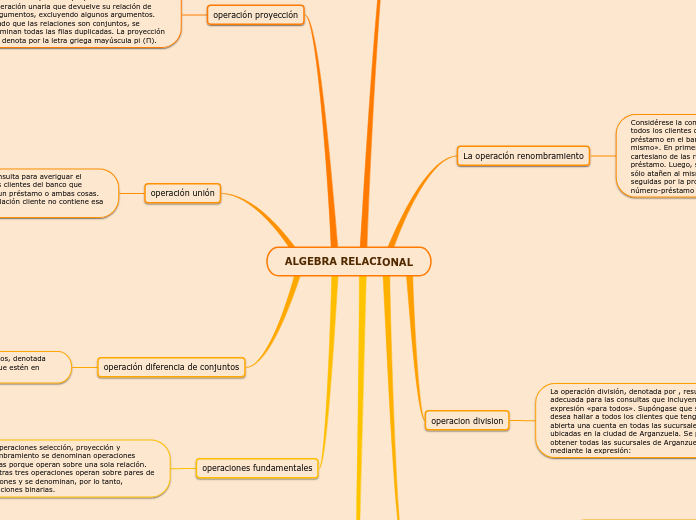
operaciones fundamentales
Las operaciones selección, proyección y renombramiento se denominan operaciones unarias porque operan sobre una sola relación. Las otras tres operaciones operan sobre pares de relaciones y se denominan, por lo tanto, operaciones binarias.
operación diferencia de conjuntos
La operación diferencia de conjuntos, denotada por –, permite buscar las tuplas que estén en una relación pero no en la otra.
La expresión r – s da como resultado una relación que contiene las tuplas que están en r pero no en s. Se pueden buscar todos los clientes del banco que tienen abierta una cuenta pero no tienen concedido ningún préstamo escribiendo:
Πnombre-cliente (impositor) – Πnombre-cliente (prestatario)
Como en el caso de la operación unión, hay que asegurarse de que las diferencias de conjuntos se realicen entre relaciones compatibles. Por tanto, para que una operación diferencia de conjuntos r – s sea válida hay que exigir que las relaciones r y s sean de la misma aridad y que los dominios de los atributos i-ésimos de r y s sean iguales.
operación unión
Considérese una consulta para averiguar el nombre de todos los clientes del banco que tienen una cuenta, un préstamo o ambas cosas. Obsérvese que la relación cliente no contiene esa información:
Πnombre-cliente (prestatario) ∪ Πnombre-cliente (impositor)
Πnombre-cliente (impositor)
También se conoce la manera de averiguar el nombre de los clientes con cuenta en el banco:
Πnombre-cliente (prestatario)
operación proyección
La operación proyección permite producir esta relación. La operación proyección es una operación unaria que devuelve su relación de argumentos, excluyendo algunos argumentos. Dado que las relaciones son conjuntos, se eliminan todas las filas duplicadas. La proyección se denota por la letra griega mayúscula pi (Π).
Πnúmero-préstamo, importe (préstamo)
Composición de operaciones relacionales
Es importante el hecho de que el resultado de una operación relacional sea también una relación. Considérese la consulta más compleja «Encontrar los nombres de clientes que viven en Peguerinos». Hay que escribir:
Πnombre-cliente ( σciudad-cliente = «Peguerinos» (cliente))
operación selección
La operación selección selecciona tuplas que satisfacen un predicado dado. Se utiliza la letra griega sigma minúscula (σ) para denotar la selección. El predicado aparece como subíndice de σ. La relación del argumento se da entre paréntesis a continuación de σ. Por tanto, para seleccionar las tuplas de la relación préstamo en que la sucursal es «Navacerrada» hay que escribir:
la relación que resulta de la consulta anterior es:
σnombre-cliente = nombre-banquero (responsable-préstamo)
Si la relación préstamo es como se muestra a continuación:
σnombre-sucursal = «Navacerrada» ∧ importe>1200 (préstamo)
En general, se permiten las comparaciones que utilizan =, ≠, o ≥ en el predicado de selección. Además, se pueden combinar varios predicados en uno mayor utilizando las conectivas y (∧) y o (∨). Por tanto, para encontrar las tuplas correspondientes a préstamos de más de 1.200 concedidos por la sucursal de Navacerrada, se escribe:
operación producto cartesiano
La operación producto cartesiano, denotada por un aspa (×), permite combinar información de cualesquiera dos relaciones. El producto cartesiano de las relaciones r1 y r2 como r1 × r2. Recuérdese que las relaciones se definen como subconjuntos del producto cartesiano de un conjunto de dominios. A partir de esta definición ya se debe tener una intuición sobre la definición de la operación producto cartesiano
Ahora que se conoce el esquema de relación de r = prestatario × préstamo hay que averiguar las tuplas que aparecerán en r. Como se podía imaginar, se crea una tupla de r a partir de cada par de tuplas posible: una de la relación prestatario y otra de la relación préstamo.
σprestatario.número-préstamo = préstamo.número-préstamo ( σnombre-sucursal = «Navacerrada» (prestatario x préstamo))
Πnombre-cliente ( σprestatario.número-préstamo = préstamo.número-préstamo ( σnombre-sucursal = «Navacerrada» (prestatario x⋅ préstamo)))
operacion division
La operación división, denotada por , resulta adecuada para las consultas que incluyen la expresión «para todos». Supóngase que se desea hallar a todos los clientes que tengan abierta una cuenta en todas las sucursales ubicadas en la ciudad de Arganzuela. Se pueden obtener todas las sucursales de Arganzuela mediante la expresión:
La operación que proporciona exactamente esos clientes es la operación división. La consulta se formula escribiendo:
Πnombre-sucursal ( σciudad-sucursal = «Arganzuela» (sucursal))
Πnombre-cliente, nombre-sucursal (impositor cuenta)
Se pueden encontrar todos los pares (nombre-cliente, nombre-sucursal) para los que el cliente tiene una cuenta en una sucursal escribiendo:
r2 = Πnombre-cliente, nombre-sucursal (impositor cuenta)
r1 = Πnombre-sucursal ( σciudad-sucursal = «Arganzuela» (sucursal))
La operación renombramiento
Considérese la consulta «Hallar los nombres de todos los clientes que tienen concedido un préstamo en el banco y averiguar el importe del mismo». En primer lugar se calcula el producto cartesiano de las relaciones prestatario y préstamo. Luego, se seleccionan las tuplas que sólo atañen al mismo número préstamo, seguidas por la proyección de nombre-cliente, número-préstamo e importe resultantes
Sin embargo, para hallar a otros clientes que vivan en esa calle y en esa ciudad hay que hacer referencia por segunda vez a la relación cliente. En la consulta siguiente se utiliza la operación renombramiento sobre la expresión anterior para darle al resultado el nombre dirección-Gómez y para cambiar el nombre de los atributos a calle y ciudad en lugar de calle-cliente y ciudad-cliente:
( σnombre-cliente = «Gómez» (cliente)))))
ρdirección-Gómez (calle, ciudad) (Πcalle-cliente, ciudad-cliente
cliente.ciudad-cliente = dirección-Gómez.ciudad (cliente ⋅
Πcliente.nombre-cliente ( σcliente.calle-cliente = dirección-Gómez.calle ∧
Considérese la siguiente consulta como un nuevo ejemplo de la operación renombramiento: «Averiguar los nombres de todos los clientes que viven en la misma calle y en la misma ciudad que Gómez». Se puede obtener la calle y la ciudad en la que vive Gómez escribiendo:
Πcalle-cliente, ciudad-cliente ( σnombre-cliente = «Gómez» (cliente))
Paso 2: La consulta para averiguar el máximo saldo de cuenta del banco puede escribirse de la manera siguiente:
Πsaldo (cuenta) – Πcuenta.saldo ( σcuenta.saldo < d.saldo (cuenta ⋅ ρd (cuenta)))
Paso 1: Para calcular la relación intermedia hay que comparar los valores de los saldos de todas las cuentas. Esta comparación se puede hacer calculando el producto cartesiano cuenta x cuenta y formando una selección para comparar el valor de cualesquiera dos saldos que aparezcan en una tupla. En primer lugar hay que crear un mecanismo para distinguir entre los dos atributos saldo. Se utilizará la operación renombramiento para cambiar el nombre de una referencia a la relación cuenta; así, se puede hacer referencia dos veces a la relación sin ambigüedad alguna.
Πcuenta.saldo ( σcuenta.saldo < d.saldo (cuenta ⋅ ρd (cuenta)))
La relación temporal que se compone de los saldos que no son el máximo
operacion reunion natural
Aunque la definición de la reunión natural es compleja, la operación es sencilla de aplicar. Como ilustración, considérese nuevamente el ejemplo «Averiguar los nombres de todos los clientes que tienen concedido un préstamo en el banco y averiguar su importe». Esta consulta puede expresarse utilizando la reunión natural de la manera siguiente:
Πnombre-cliente, número-préstamo, importe (prestatario préstamo)
A diferencia de las relaciones de la base de datos, los resultados de las expresiones de álgebra relacional no tienen un nombre que se pueda utilizar para referirse a ellas.- Resulta útil poder ponerles nombre; el operador renombramiento, denotado por la letra griega rho minúscula (ρ), permite realizar esta tarea.
(prestatario X préstamo))
( σprestatario.número-préstamo = préstamo.número-préstamo
Πnombre-cliente, préstamo.número-préstamo, importe