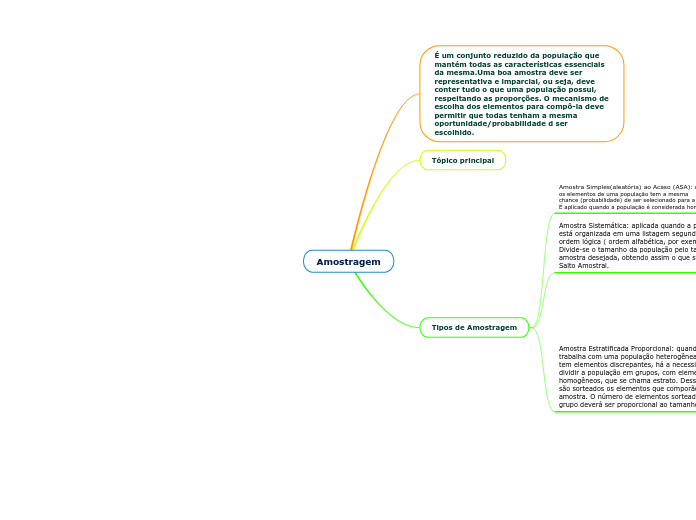
Amostragem
Tipos de Amostragem
Amostra Estratificada Proporcional: quando se trabalha com uma população heterogênea, onde se tem elementos discrepantes, há a necessidade de se dividir a população em grupos, com elementos homogêneos, que se chama estrato. Desses estratos são sorteados os elementos que comporão a amostra. O número de elementos sorteados de cada grupo deverá ser proporcional ao tamanho do grupo.
cálculo do tamanho da Amostra: Para se calcular o tamanho
de um amostra, ou o número necessário de pessoas a ser entrevistada. Para que se obtenha a precisão estatística desejada, são levados em conta as variáveis:
Erro máximo permitido: Os resumos obtidos numa pesquisa elaborada a partir de amostras não são rigorosamente exatos em relação ao universo. Esses resultados apresentam sempre um erro de medição. Nas pesquisas sociais trabalha-se usualmente com uma estimativa de erro entre 3 e 5%. Quanto maior a amostra, menor a margem de erro. Porém, quando maior a amostra, mais complexa e dispendiosa a pesquisa se torna.
Porcentagem com que o fenômeno se verifica: Quando existe uma informação prévia a respeito da resposta que se pretende encontrar, está informação pode ser utilizada para diminuir o tamanho da amostra. Quando não é possível fazer essa estimativa, adota-se a probabilidade média de 50%. Com esses 4 fatores podemos adotar uma fórmula matemática para o cálculo do tamanho da amostra ideal. Para a população Finita, ou seja, quando a população pesquisada não supera 100.000 indivíduos, a fórmula para o cálculo do tamanho da amostra é:
n= D2.p.q.n
e2.(N-1)+D2.p.q
Onde: n= Tamanho da amostra ( número de pessoas que deverão participar da pesquisa);
D= Número de desvios padrão adotado (1,2 ou 3);
p e q= Porcentagem em que o fenômeno se verifica ( na maioria dos casos 50 e 50);
N= Tamanho da população ( número total de pessoas que fazem parte do grupo de pesquisa);
e= Erro percentual máximo permitido (p.ex,:2,3,5);
Para População Infinita, ou seja, quando a população pesquisada supera 100.000 indivíduos, a fórmula para o cálculo do tamanho da amostra é a seguinte:
n=D2.p.q
e2
Onde: n= Tamanho da amostra( número de pessoas que deverão participar da pesquisa);
D=número de desvio padrão adotado (1,2 e 3);
p e q= Porcentagem em que o fenômeno se verifica (na maioria dos casos 50 e 50);
e= Erro percentual máximo permitido (p.ex.:2,3,5);
Lembrete: Estes cálculos servem apenas para definir qual número de pessoas deve ser consultado em uma pesquisa quantitativa por amostragem. Para garantir o bom resultado da pesquisa este número deve ser utilizado em conjunto com um Tipo de Amostra. Caso o tipo utilizado seja a Amostra Estratificada Proporcional é mais importante saber quem do que quantas pessoas participarão da pesquisa.
Nível de confiança desejado: O nível de confiança de uma amostra refere-se a área da curva normal definida a partir dos desvios padrão em relação á sua média. Significa qual a porcentagem da população estará representada na amostra.
1. desvio padrão = 68% de representatividade
2. desvios = 95,5% de representatividade
3. desvios = 99,7% de representatividade
A. Amplitude do Universo: Os universos de pesquisa podem ser finitos ou infinitos, convencionou-se que os finitos são aqueles cujo número de elementos não excede a 100.000. Universos infinitos, por sua vez, são aqueles que apresentam elementos em número superior a esse.
Amostra Sistemática: aplicada quando a população está organizada em uma listagem segundo alguma ordem lógica ( ordem alfabética, por exemplo). Divide-se o tamanho da população pelo tamanho da amostra desejada, obtendo assim o que se chama de Salto Amostral.
Amostra Simples(aleatória) ao Acaso (ASA): quando todos
os elementos de uma população tem a mesma
chance (probabilidade) de ser selecionado para a amostra.
É aplicado quando a população é considerada homogênea.
Tópico principal
É um conjunto reduzido da população que mantém todas as características essenciais da mesma.Uma boa amostra deve ser representativa e imparcial, ou seja, deve conter tudo o que uma população possui, respeitando as proporções. O mecanismo de escolha dos elementos para compô-la deve permitir que todas tenham a mesma oportunidade/probabilidade d ser escolhido.