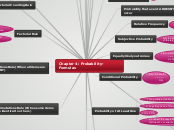
Chapter 4: Probability-Formulas

もっと見る

Noun Plural

Tanya Mikusにより

UFC

Ian Priskićにより

Exponential functions

Mya Morgan - Sandalwood Heights SS (2442)により

Nassim Nicholas Taleb: A Crazier Future

Paweł Badeńskiにより

Chapter 4: Probability-Formulas

Combinations Rule

"different combinations" or "order doesn't matter"

# of combinations (order doesn't count) when n diff. items are available, but only r of them are selected w/o replacement

nCr=n!/(n-r)!r!

Permutations Rule (When some items are identical to others)

10 letters (aaaabbccde) are available and all are selected, the # of diff. premutaions is: 10!/4!2!2!

# of diff. permutations when n items are available and all n are selected w/o replacement, but some of the items are identical

n!/(n_1 !n_2 !⋯n_k !)

Permutations Rule (When all items are DIFFERENT)

"If 5 letters are available, and 3 are to be selected w/o replacement"

# of diff. permutations when n diff. items are available, but only r of them are selected w/o replacement

nPr= n! ------ (n-r)!

Factorial Rule

"the # of ways five letters can be arranged" 5!:5*4*3*2*1

n!: # of diff. permutations (order counts) of n diff. items when all n of them are selected

Factorial Counting Rule

"How many different characters are possible if they're all represented" Ex: 00110111: 2^8=720

m*n=# of ways 2 events can occur

Independent

Occurrence doesn't affect probability: Sampling w/ replacement

Factorial symbol: !

Special: 0!=1

Example: 3!=3*2*1

Sampling w/o replacement

Depedent

Probability of event B occurring after it is assumed that event A has already occurred

P(A and B)= P(A)*P(B) (independent)

P( A and B)=P(A)*P(B|A) (dependent)

Intuitive Addition Rule

Intuitive Addition Rule= P(A)+P(B) --------------------------------------------- total # of outcomes in the sample space

Rule of Complementary Events

P(A)=1-P(Ā)

P(Ā)=1-P(A)

P(A)+P(Ā)=1

Formal Addition Rule

P(A or B)= P(A) + P(B) - P(A and B)

Probability of At Least One

4) Subtract the result from 1 P(at least 1 occurrence)= 1-P(no occurrences)

3) Find P(Ā)

2) Ā= getting none of the event

1) A= getting at least one of some event

Conditional Probability

P(B|A)= P(A and B) ------------ P(A)

"given that..."

Intuitive: P(B|A)

Equally likely outcomes

P(A)= # of ways A can occur ------------------------- # of different simple events

Subjective Probability

P(A) is estimated by knowledge of the relevant circumstances

Relative Frequency

P(A)= # of times that A occurred ------------------------------ # of times trial was repeated

Probability that event A DOESN'T occur

P(Ā)

Probability of event A

P(A)

Unusual: Extreme result

# of outcomes is far above/below typical values

Unlikely event

Probability= 0.05 or less

Multiplication

And= multiplication

P(A and B)

Addition

Or=addition

P(A or B)

Disjoint (Mutually Exclusive)

Two events cannot occur at the same time