によって yassary salas 1年前.
72
もっと見る
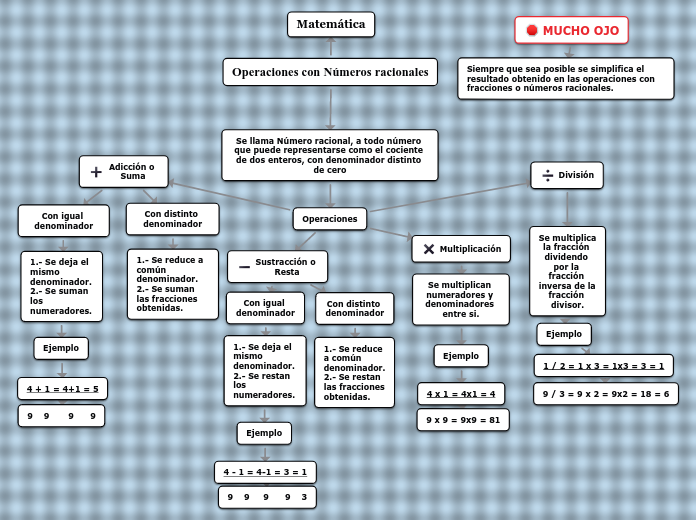
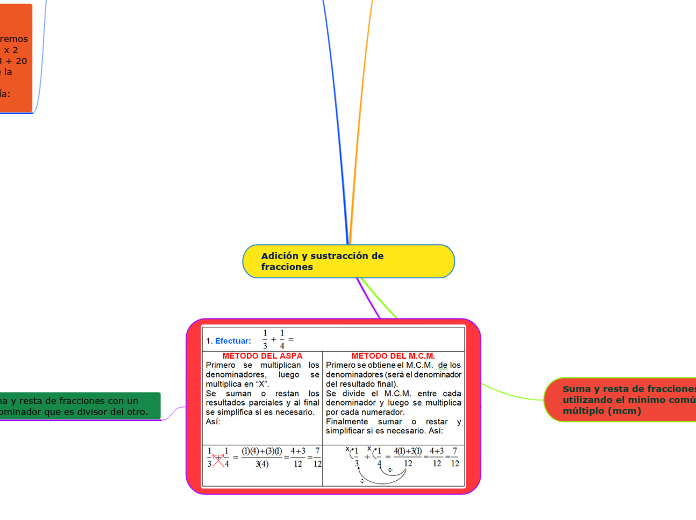
Operaciones de los números Racionales. Suma y resta: Para sumar o restar fracciones, es necesario que los denominadores sean iguales. Si los denominadores son diferentes, se deben encontrar equivalentes con el mismo denominador. Una vez que los denominadores son iguales, se suman o restan los numeradores y se mantiene el denominador común. 2. División: Para dividir fracciones, se multiplica la primera fracción por la inversa de la segunda. La inversa de una fracción se obtiene intercambiando el numerador y el denominador.
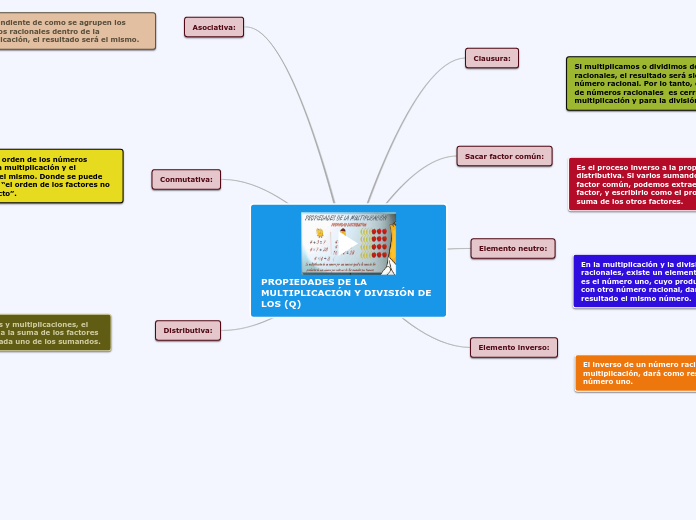
Propiedades de los números Racionales. • Conmutatividad: La suma y la multiplicación de dos números racionales son conmutativas, es decir, el orden en que se suman o multiplican los números no cambia el resultado. Por ejemplo, a + b = b + a y ab = ba. • Asociatividad: La suma y la multiplicación de tres o más números racionales son asociativas, es decir, el resultado es el mismo independientemente de cómo se agrupen los números. Por ejemplo, (a + b) + c = a + (b + c) y (ab)c = a(bc). Elemento neutro: El número 0 es el elemento neutro para la suma de números racionales, es decir, a + 0 = a para cualquier número racional a. El número 1 es el elemento neutro para la multiplicación de números racionales, es decir, a × 1 = a para cualquier número racional a. Elemento opuesto: Para cada número racional a, existe un número racional opuesto -a tal que a + (-a) = 0. Distributivita: La multiplicación es distributiva sobre la suma, es decir, a(b + c) = ab + ac para cualquier número racional a, b y c. Propiedad inversa: Cada número racional distinto de cero tiene un inverso multiplicativo, es decir, para cualquier número racional a distinto de cero, existe un número racional b tal que ab = 1.
Relación de orden. Los números racionales pueden ser ordenados utilizando el mismo criterio de ordenamiento que se utiliza con los números enteros. Es decir, si tenemos dos números racionales diferentes, podemos compararlos para determinar cuál es mayor o menor. Para hacer esto, se comparan los numeradores de los dos números, y si son iguales, se comparan los denominadores. Si los numeradores son diferentes, el número con el numerador mayor es el mayor de los dos. Si los numeradores son iguales, el número con el denominador menor es el mayor de los dos.
PROPIEDADES DE LOS NUMEROS ENTEROS CLAUSURATIVA: La suma obtenida al adicionar números es un número entero. CONMUTATIVA: En toda adición el orden de los sumandos no altera la suma. ASOCIATIVA: Al asociar dos o más sumandos de una adición en distintos orden la suma no se altera. PROPIEDAD DEL OPUESTO ADITIVO: Todo número entero adicionado con su opuesto aditivo da como resulto cero.
LEY DE LOS SIGNOS IMPORTANTE: La ley se basa en lo siguiente: si los signos son iguales el resultado debe ser positivo. En cambio si los signos son diferentes el resultado será negativo. En otras palabras podría decirse que signos iguales se suman, signos diferentes se restan. Esto va relacionado en operaciones básicas con números enteros.
OPERACIONES DE LOS NUMEROS ENTEROS Suma de números enteros: Si los dos enteros a sumar tienen el mismo signo se suma los números siguiente signo y se conserva el signo. EJEMPLO: (+4) +(-5) =-1 Resta de números enteros: Cuando tenemos una resta de enteros, podemos transformarla en una suma cambiando el signo del segundo sumando. Multiplicación y División de enteros: La multiplicación de dos enteros se calcula multiplicando los números sin signo y aplicando la regla de los signos. La división de enteros se calcula dividiendo los números sin signo y aplicando la regla de los signos.
Operaciones de los números Reales. • Suma: El resultado de sumar dos números reales es otro número real. • Diferencia: La diferencia de dos números reales se define como la suma del minuendo más el opuesto del sustraendo. • Producto: El producto de dos números reales es otro número real. • División: La división de dos números reales se define como el producto del dividendo por el inverso del divisor, La división o cociente es la operación inversa de la multiplicación y consiste en averiguar cuántas veces un número (divisor) está contenido en otro número (dividendo). Si divides 20 (dividendo) entre 5 (divisor), el resultado es 4 (cociente), porque 20 ÷ 5 = 4; 4 × 5 = 20. • Potenciación: La potencia es el resultado que se obtiene al multiplicar un número dos o más veces por sí mismo. En particular, la potencia dos, o cuadrado, de un número se obtiene al multiplicarlo por sí mismo y se denota escribiendo un dos pequeño en la parte superior derecha de dicho número. Por ejemplo, el cuadrado de cinco se escribe de la siguiente forma: 52 = 5 × 5 = 25; y el cuadrado de menos tres se escribe –32 = –3 × –3 = 9. • Logaritmación: Logaritmación es el proceso de hallar el exponente al cual fue elevada la base para obtener un número. • Radicación: La operación inversa de la potencia, que es la raíz. Esto significa que
Los intervalos no acotados son intervalos cuyo principio está bien marcado pero el extremo final siempre estará al infinito ya sea negativo o positivo, estos a su vez se dividen en: intervalo no acotado cerrado en A hacia el infinito positivo, intervalo no acotado abierto en A hacia el infinito positivo, intervalo no acotado cerrado en A hacia el infinito negativo y el intervalo no acotado abierto en A hacia el infinito negativo.
Los intervalos acotados Son los intervalos cuyos extremos se encuentra en una serie de combinación entre abiertos y cerrados pero con un final marcado entre los dos puntos a y b, estos a su vez se dividen en: intervalos acotados cerrados, intervalos acotados abiertos y en intervalos acotados semi abiertos o semi cerrados
Operaciones de los números Irracionales. Con los números irracionales también se realizan operaciones básicas de suma, resta, multiplicación y división. Para realizar las diferentes operaciones básicas, se deben considerar algunas de las propiedades antes mencionadas para números irracionales. Para sumar o restar números irracionales, se puede realizar verificando si sus radicales son semejantes, es decir, que los radicales tengan el mismo índice y la misma cantidad sub radical. De ser radicales semejantes, se suman o restan los coeficientes, según el caso y se coloca el radical semejante. De ser necesario se simplifica
Aplicaciones de los números Irracionales. Calcular circunferencias. El número irracional π es usado para calcular la circunferencia de un círculo. Para ello se utiliza la fórmula C=πd en la que se multiplica el diámetro por el número pi. Esta función es indispensable para la fabricación de elementos de uso cotidiano como relojes, ruedas y discos de vinilo. También se usa para realizar las figuras geométricas de un campo de fútbol. Construir estructuras cilíndricas. Se usa el número irracional π dentro del ámbito de la construcción para realizar estructuras con forma de cilindro. También se usa para fabricar elementos o bienes con esa forma, como velas, rollos de papel, botellas, garrafas, latas, entre otros.
Racionalización Se llama racionalización de una expresión fraccionaria al procedimiento mediante el cual se logra que el denominador sea un número racional. Entonces multiplicamos al numerador y al denominador por 7 , no se altera el cociente dado y el denominador queda racionalizado..
Operaciones de los números Irracionales Multiplicación de irracionales Para multiplicar números irracionales, se puede realizar aplicando la propiedad de radicales para raíces de igual o de diferente índice o simplemente expresar en forma de número decimal cada radical y multiplicar. División de irracionales Al igual que en la multiplicación se procede aplicando la propiedad de radicales, ya sea para raíces de igual o diferente índice y se simplifica de ser posible.
