Differential Equations and Linear Algebra

もっと見る

Trigonometric Ratio

Williams Shireeceにより

Solving Log Functions:

Ali Rizviにより

VM266 1418

John Krauseにより

Differential Equations Final

Zach Jonesにより

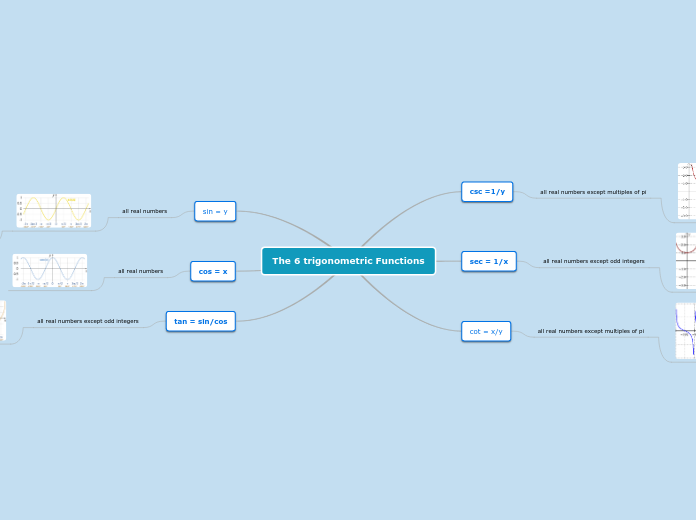
Do you need to solve a differential equation?

Do you have a step function and initial conditions? If yes, use Laplace

Is it a first order differential equation?

Is the DE separable?

If not, use the Integrating Factor Method (click play for video tutorial)

If yes, solve by using Separation of Variables (click play for video tutorial)

Main topic

Is it a system of first order DE's?

use the eigenvalues/eigenvectors method

Is it a second order differential equation?

Is it homogenous?

If yes, does it involve complex roots?

If it involves complex roots, follow this video. (Homogenous with imaginary roots)

If not, follow this video. (Homogenous with real roots)

If not, you will need the particular solution added to the homogenous solution.

To get the homogenous solution, follow this video

To get the particular solution, you'll need to identify the driving force. What type of function is the driving force?

If it's a combination of any of these, follow this video (multiply them together)

If it's an exponential function, follow this video. Ae^t

If it's a trigonometric function, follow this video. (Acost + Bsint)

If it is a polynomial, follow this video. Remember to add it on to the homogenous solution. At^2 + Bt + C