によって Luisa Fernanda Rueda Estupiñan 4年前.
311
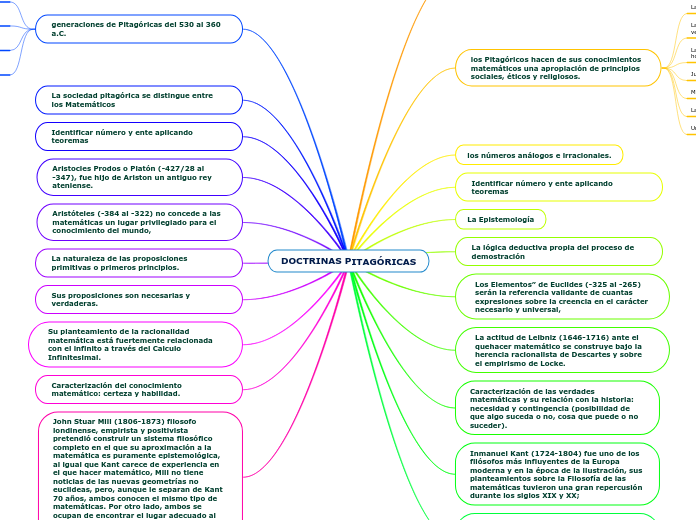
DOCTRINAS PITAGÓRICAS
La doctrina pitagórica, originada en Cretona, considera los números como principios fundamentales y distingue entre matemáticos y seguidores religiosos. Los pitagóricos, a través de generaciones, han influido en el estudio de las matemáticas mediante la identificación y aplicación de teoremas.