Elementary School Mathematics
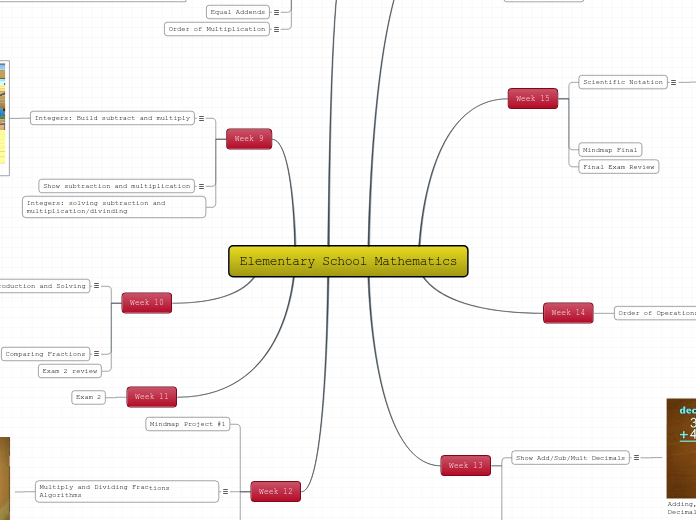
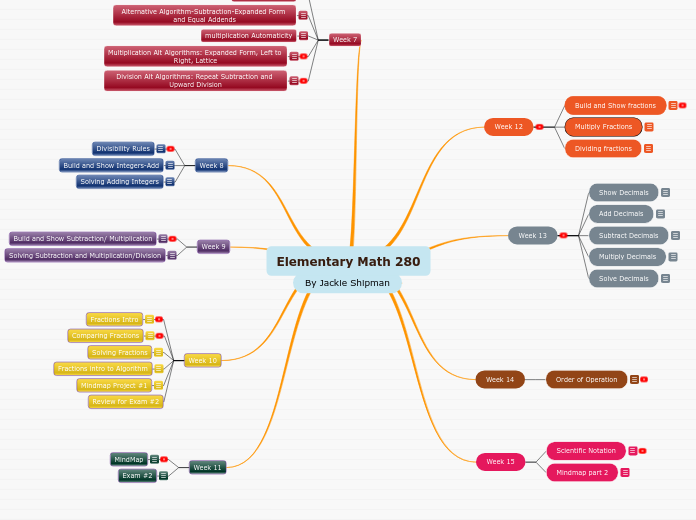
Week 12
Building and Showing Fractions
Building and Showing Fractions:
To show our fractions we will have to build diagrams.
Given: 1 + 1
3 4
We have to draw each fraction going a different way, meaning the first fraction has to be drawn going vertical, and the second fraction has to be drawn going horizontal.
Then, we will draw another box, we will need to make sure we can add our two fractions. The same size pieces need to be in the diagram. In this case we will have to have 12 different boxes in our diagram. We will fill in the amount of rows we need. For our first fraction itll be one, then the second one will need to fill up 4 boxes. We add those two up and get 7. Then we will count the overall boxes we have and that is 12. So our answer is 7/12.
Multiply and Dividing Fractions Algorithms
Multiple and Dividing Fractions Algorithm:
Multiplication:
We are given: 8 X 3
10 4
Next, we have to break down each number we have (Simplified).
8 is multiplied by 2 and 4, 3 will stay the same. 10 will be 2 and 5, and 4 will stay the same.
Then, we find out funky ones, meaning what factors of each number we broke down are the same. In this case the numbers 2 and 4 will get crossed out. This leaves us with 3 on the top and 5 on the bottom. So we will multiple across and get 3/5.
Division:
We are given: 8 ÷ 3
10 4
So, we will do K:eep C:hange F:lip
K C F
8 ÷ 3
10 4
Our division symbol will turn into multiplication and 3/4 will be 4/3.
K C F
8 x 4
10 3
Then, we will break down out numbers the same way we solved our multiplication problem. Keeping in mind our funky ones, and crossing those out. Then we will multiple across and get our answer.
Multiply and Dividing Fractions
Mindmap Project #1
Week 11
Exam 2
Week 10
Exam 2 review
Comparing Fractions
Comparing Fraction:
For this, we will be using signs that are less than, greater than, and equal too signs, < = >.
If a fraction has a whole number in front of it, depending on the whole number is where the less than greater than sign will be facing.
Anchor Fractions, are fractions that we know then off the bat, 1/2
Doubling the top number, if its bigger than the denominator means its over 1/2, if its less then its less than 1/2.
Ex:
7/13 11/23
doubled
14/13 22/46
so, we know that 14/13 is the greater.
7/13 > 22/46
Next:
2/9 2/7
For this 2/7 is greater because of the number of pieces.
2/9 < 2/7
Then:
If we were to draw out the fractions, it will help us understand the sizing. When we see fractions that are almost whole numbers.
Fractions: Introduction and Solving
Intro to fractions:
4 ->The number of things we have
6 ->Size of pieces
Solving:
When solving fractions the thing to notice to do the easy problems first.
Ex: 14 + 5 1/3
=19 1/3
Since there wasn't a fraction attached to the first number you can just add across.
When given this problem 2/9 + 3/9, this means we have the same size pieces, so we add across or subtract, but keep the bottom number the same. 5/9
Fraction Introduction
Week 9
Integers: solving subtraction and multiplication/divinding
Show subtraction and multiplication
Showing Subtraction and Multiplication:
When showing subtraction using the actual symbols for negative and positive and using their colors, blue for positive and red for negative.
This is the same as building out the problems, the only different is using the actual signs for negative and positive.
Integers: Build subtract and multiply
Building Subtraction and Multiplication :
The best way to start with subtraction is to figure out what the best way to say the problem out.
-4-(-3)
This is 4 negatives take away 3 negatives.
Using the colors red and yellow for the negative and positives will help when building these problems out.
Zero Banks:
These are as big as we need them to be, or big enough. We use them to help us see the numbers we need to take away.
When given a problem, use the counters. If given -3 use three red counters, so it shows its a negative number. Given 5, use 5 yellows.
Building Subtraction
Week 7
Order of Multiplication
For this chapter we learned about Times Tests. We learned that they aren't efficient for helping students learn how to multiply. Instead, they show that students dont learn their times table and will eventually forget it. Research show's that these are not the best ways to show children their times table.
Multiplication:
The best way to learn multiplication facts are by starting with
1s, 2s, 10s, and 5s.
Next is 3s, 9s, and the doubles.
Lastly they need to learn 4s, 6s, 7s, and 8s
Left to Right:
Rewriting the problem from left to right. Then multipleyou s the numbers on the bottom left first. The work your way to the right.
4 2
|/ \|
1 3
400
20
6
120
546
Lattice:
This is where you set up the lattice. We create a box. You have to make sure one number is on the top, and the other on the right hand side.
2 0
| / 8 | / 0 |4
| / 4| / 0 |2
8 / 4 / 0 = 840
Equal Addends
Equal Addends, this is where the idea is used in subtraction. The problem is rewritten, and turn one of the numbers so that its easier to subtract. As long as you add the equal amount to both numbers, you can add whatever you want. You have to do the same number to both of the numbers you are subtracting.
Ex: 43-17
43+3 = 46
-17+3 = 20
26
Expanded Form
Expanded form is when you expand the numbers to their whole number to make subtracting easier.
Ex: 459-324
400+50+9
-300+20+4
100+30+5 =135
Spiraling content
Spiraling is when you re-visit the previous learned content. This is so that students are able to learn the content over a number of weeks.
Week 13
Solving Decimals
Solving Decimals:
To start these problems we will first need to estimate what our answer might be.
Subtraction
When given a problem to subtract, 123.45-67.23 we will put it in this formate.
123.45
- 67.23
Then we will subtract the way we know how.
173.45
- 62.23
111.22
Addition
We will start with estimating what we think our answer will be.
Then we will do the exact same thing as subtracting. Lining up our whole numbers as we go and our decimal places.
Multiplication:
To start these problems we will first need to estimate what our answer might be.
Then we will multiply without our decimal places.
105
x 40
42.00
Then we add our decimal place back.
Show Add/Sub/Mult Decimals
Showing how to Add, Sub, Mult Decimals:
When showing how to add, subtract, and multiply decimals, we will be using manipulatives, or drawings.
Scenario 1: When given 0.3+0.2 you notice that these two numbers are smaller than 10. So we will build a diagram with 10 rows. Then we will shade in 3 rows, then 2 rows. At the end of the shading we should get our answer. We added straight ahead because the two numbers were the same size pieces.
Scenario 2: When given 0.14+0.13 we notice that they are not a single digit number. In this case we have tenths and hundreds. W will start with building a diagram with 10 rows going vertical. Then we create 10 more rows going horizontal. We star to shade in our numbers. 0.14 has a 1 in the hundreds place, so we shade 1 row going vertical, then 0.13 we shade another row. That means 2 rows are shaded. Then we will place a dot for every tenths place we have. In 0.14 case we have 4, so we will add 4 dots, one dot per square. These dots should be going vertical. Then we add 3 more for out 0.13. After we finish those dots, we can count how many rows we have shaded in. In this case we have 2, then we count out dots, 7. We added them together and get 0.27.
Scenario 3: When working with subtraction, if we get a problem like 0.25-0.12 we will start with our same diagram in Scenario 2. Next we will fill in out number 0.25. We wont add 0.12 because that is what we will be taking away. Once we have out diagram filled out we will start taking away. 0.12 have a tenths and a hundreds. We will take away 1 vertical row hundreds, leaving us with just 1 row. Then we will take away 2 vertical dots. This will leave us with our answer, 0.13.
Scenario 4: For multiplication we have 0.3(0.2). We will build a diagram with only 10 vertical rows. Then we will shade in 3 rows. Leaving one row in between each shaded row. Next we will add 10 rows horizontally. We will shade in 2 rows horizontally with a space in between each row. Next our answer will be the double shaded region, or where the two rows meet. Our answer is 0.6.
Adding, Subtracting, and Multiplying Decimals
Week 14
Order of Operations
Order of Operations
Is defined as the order in which we are allowed to do our mathematics.
PEMDAS :the order in which you need to do your mathematics.
P: Parenthesis
E: Exponents
M: Multiplication
D: Division
A: Addition
S: Subtract
Multiplication and Division are on the same level
Addition and Subtraction are on the same level
Grouping:
EXP
D/M or M/D, whichever comes first, left to right.
A/S, left to right
Week 15
Final Exam Review
Mindmap Final
Scientific Notation
Scientific Notation:
During week 15 we learned about scientific notation and how to get a number from standard form to scientific notation. Also how to get a number thats already in scientific notation back to standard form.
First, scientific notation is used in science, or really big or really small numbers. These are numbers are are used when you measure atoms, how long it takes to travel to the moon, and in chemistry.
Then, a scientific notation number has to be between 1-10, and there will also be a decimal. These numbers can be either negative or positive. There is a times 10, plus an exponent (number). The exponent can be positive or negative.
EX: 1.4X102
When given the number 2,450,000,000. You see that this number is a BIG number, given 0.00000345, you notice that this number is really SMALL. These both numbers have to be smaller or bigger than 1.
If you have a BIG number, this means that your exponent is positive.
If you have a SMALL number, this means that your exponent is negative.
The decimal point belongs between the first two non zero numbers. Then you count how many decimal places you have after your last zero.
EX: 2,450,000,000 will equal 2.45 X 109
Week 8
Intro to Integers
Integers:
Any numbers that have positive or negative value.
Having two colored counters will be able to help show what you are building. Preferably red and yellow counters, or two different counters.
When going to add integers make sure the right color of your counter is showing. Plus keep in mind zero pairs. A zero pair is when you add integers together that cancel each other out.
Positives belong on top of negatives.
Red=Negative, Yellow= Positive
EX:
000 Here we have the number 1
00
Divisibility Rules