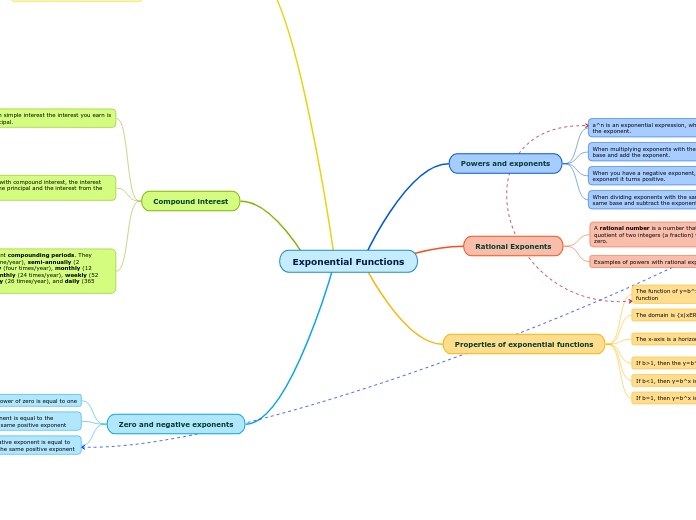
Exponential Functions
Zero and negative exponents
Any fractional base raised to a negative exponent is equal to its reciprocal of the base raised to the same positive exponent
For example: (a/b^-m)= b/a^m
Any base raised to a negative exponent is equal to the reciprocal of the base raised to the same positive exponent
For example: 2^-4/3^-4=3^4/2^4
Any value raised to the power of zero is equal to one
For example: 7^0=1
Compound interest
There are many different compounding periods. They include annually (1 time/year), semi-annually (2 times/year), quarterly (four times/year), monthly (12 times/year), semi-monthly (24 times/year), weekly (52 times/year), bi-weekly (26 times/year), and daily (365 times/year).
Compound interest: with compound interest, the interest you earn is based on the principal and the interest from the previous period.
For example: $5000 is invested at 8% compounded quarterly. By looking at this statement you know that the principal amount is $5000, the interest is 0.02 (you divide the given interest by four because it is compounded quarterly), and the n value is 20 because it is compounded quarterly for five years (4x5=20). You solve this by substituting all the values into the formula, and you should get a=$7429.74.
The formula for compound interest is A=P(1+i)^n
A is the amount of principal and interest, P is the present value of the investment or debt, i is the rate of interest per period, and t is the total number of periods
Your principal amount for the next period is the same as your final amount for the previous period.
Simple Interest: With simple interest the interest you earn is based only on the principal.
The formula for simple interest is: I=prt
I stands for simple interest, p stands for principal amount, r stands for annual rate, and t is time in years.
Power of power
For example: (a^3)^2= (a^3)(a^3)=a^6
When raising a power to another power the exponents get multiplied
When raising an exponent to a power it is just like raising a regular number to a power
Properties of exponential functions
If b=1, then y=b^x is a straight line
If b<1, then y=b^x is a straight line
If b>1, then the y=b^x is continuously decreasing
The x-axis is a horizontal asymptote
Asymptote is a line/value that you get closer and closer to but never reach. The line of the graph gets closer and closer to the x-axis but never touches or crosses it.
The domain is {x|xER}, and the range is {y|y>0 yER}
The function of y=b^x where b>0 defines an exponential function
Rational Exponents
Examples of powers with rational exponents: x^n/m
n is a natural number, x>0 when n is a even number, if x<0, n must be an odd number.
A rational number is a number that can be expressed as the quotient of two integers (a fraction) where the divisor is not zero.
For example: 0.75, -3/4, -2.
Powers and exponents
When dividing exponents with the same base, you keep the same base and subtract the exponents.
For example: 3^6/3^2=3^4
When you have a negative exponent, you put one over the exponent it turns positive.
For example: 3^-2=1/3^2=1/9
When multiplying exponents with the same base, you keep the base and add the exponent.
For example: 2^2 x 2^2=2^4
a^n is an exponential expression, where a is the base and n is the exponent.