によって LaShundra Bell 14年前.
307
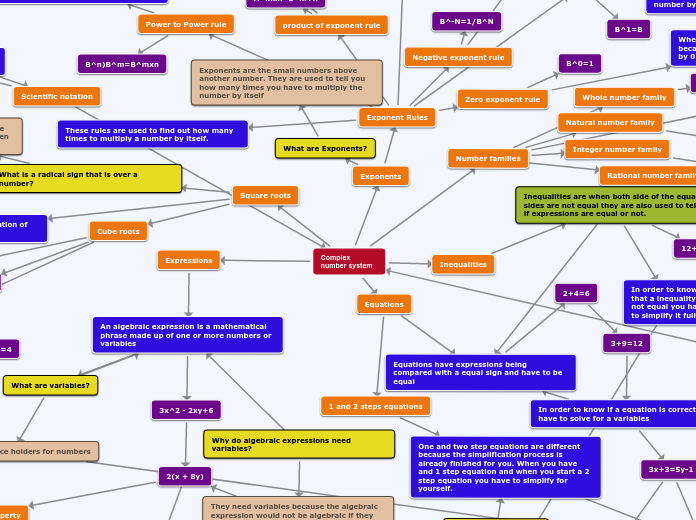
Finished chapter 6 & 7 notes
The notes cover various mathematical concepts and their applications, particularly focusing on percentages, proportions, ratios, and rates. The application of percentages includes solving problems using both proportions and equations, emphasizing the identification of key terms like "