によって Natalia Bernal Mendoza 3年前.
460
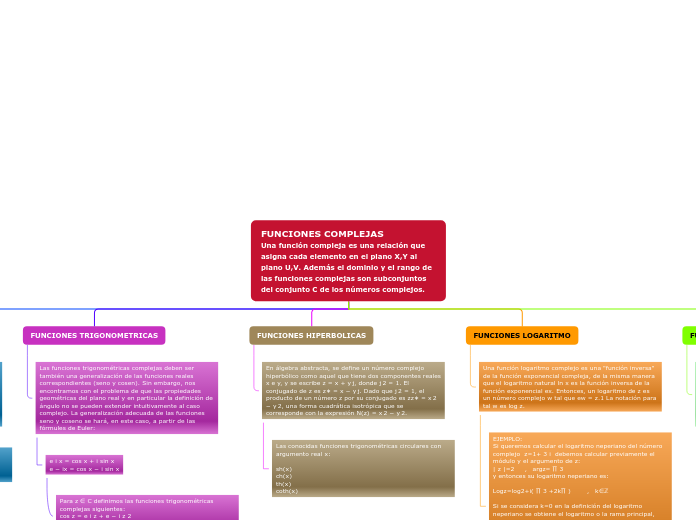
FUNCIONES COMPLEJAS Una función compleja es una relación que asigna cada elemento en el plano X,Y al plano U,V. Además el dominio y el rango de las funciones complejas son subconjuntos del conjunto C de los números complejos.
Las funciones complejas son relaciones que asignan elementos en el plano de números complejos a otros puntos en el mismo plano. Estas funciones incluyen variantes complejas de las funciones trigonométricas y exponenciales que conocemos en el ámbito real.