によって Darleny Moya 4年前.
527
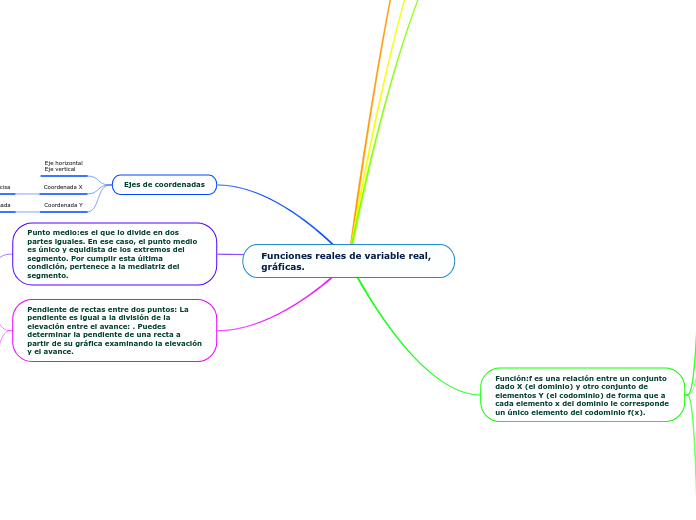
Funciones reales de variable real, gráficas.
El texto trata sobre varios conceptos fundamentales en matemáticas y geometría analítica. Se explica cómo calcular la distancia entre dos puntos utilizando la fórmula de la raíz cuadrada de la suma de los cuadrados de las diferencias de sus coordenadas.