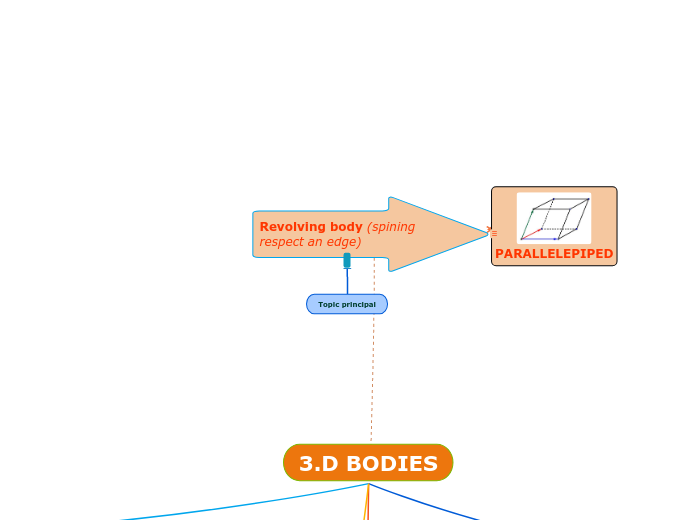
Geometry
Circles
If 2 tangent segments to a circle share a common endpoint outside the circle, then the 2 segments are congruent.
If a line in plane of a circle is perpendicular to a radius at the endpoint to a circle.
If a line is tangent to a circle, the line is perpendicular to the radius @ the point of tangency.
circles in the coordinate plane : (x-h) squared + (y-k) squared = r squared
(p+q)p=tsquared
(w+x)w=(y+2)y
segment lengths --- a*b=c*d
circumference
radius
locus
tangent to a circle
point of tangency
arcs
intercepted arc
Secants
Chords
Proofs
2 column
flow
paragraph
triangles
Pythagorean Theorem- If a triangle is a right triangle, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
HL
Triangle sum theorem
SAS
SSS
AA~
AAS
Surface Area=LA + 2B
Lat. Area=1/2PBl
area=1/2bh
volume= 1/3bh
equilateral triangles
acute triangles
If the square of the length of the longer side of a triangle is greater than the sum of the other two sides then the triangle is acute.
obtuse triangles
If the square of the length of the side of a triangle is greater than the sum of the squares of the lengths of the other two sides, then the triangle is obtuse.
Right triangles
45-45-90 triangles
In a 45-45-90 triangle both legs are congruent and the length of the hypotenuse is square root of 2 times the length of the leg
scalene triangles
30-60-90 triangles
In a 30-60-90 triangle the length of the hypotenuse is twice the length of the shorter leg. the length of the longer leg is square root of 3 times the length of the shorter leg.
isosceles
Volume
cones
rectangular prisms
bwh
spheres
4/3(pi)r3
pyramids
1/3bh
cylinders
(pi)r2h
similar solids have a ratio of a3:b3
V-bwh
Area
The length of an arc of a circle is the product of the ratio measure of arc/360 and the circumference of the circle.
A=1/2ap
A=bh
C=2(pi)r
C=(pi)d
A=1/2h(b1 +b2)
A=1/2b2(sinA)
A= 1/2 bh
A=1/2 d1d2
arc length
segment of a circle
central adjacemt arcs
apothem
concentric circle
congruent arcs
diameter
sector of circle
Trigonometry
45,45,90=x:x:2x
cosine
adjacent____hypotenuse
tangent
opposite____adjacent
sine
opposite___hypotenuse
Congruency
If a transversal intersents two parallel lines, then alternate interior and alternate exterior angles are congruent
If a transversal intersects two parallel lines, then corresponding angles are congruent.
All right angles are congruent
If 2 angles are supplements/compliments of the same angle (or 2 congruent angles)then the 2 angles are congruent
SAS,ASA,AAS,SSS,CPCIP
Vertical angless are congruent
Angles
M
Perpendicular Lines form right triangles
Acute
Obtuse
alternate interior angles are =
Same Side Interior Angles
Corresponding Angles Postulate
Alternate Exterior Angles
parallel lines
skew lines
Angle Measures
~=angles
Angles in transversals
Adjacent
Supplementary
Right
Vertical
Complementary
Conditional Statements
~q-->~p
~p-->~q
q-->p
p-->q
law if detachment
law of syllogism
biconditional
conditional
inverse
negation
counterexample
contrapositive
converse
theorem
deductive reasoning
inductive reasoning
Polygons (regular)
6-11
6-5
6-3
6-4
6-22
6-15
6-7
6-12
6-13
6-8
6-21
consecutive angles
parrallelogram
diagonals are congruent
4 right angles
rhombus
diagonals are perpendicular
4 congruent sides
diagonals bisect
polygon
equilateral/equiangular
base angle
square
leg of a trapezoid
rectangle
coordinate proof
opposite angle
kite
quadrilateral with 2 pairs of consecutive sides congruent and no opposite sides are congruent
regular polygon
base
trapezoid
exactly 1 pair of parallel sides (bases)
midsegment of a trapezoid
oppostie sides
isoscles trapezoid
2 sides that are congruent and a pair of angles that are congruent
Transformations
A translation or rotation is a compostion of two reflections
There are only 4 isometry
dialation
enlargement
reduction
center
scale factor
scale factor translations
pre-images
tessellation
isometry
point/line/rotation/reflectional symmetry
line of reflection
reflections
symmetry
reflectional symmetry
line symmetry
point symmetry
angle rotation
translational symmetry
center of a regular polygon
rotations
translation made of 2 reflections
Parallelograms
Opp. Sides ~=
Diagonals bisect Opp
Consecutive angles supp.
Opposite Sides
Opposite Angles
Consecutive Angles