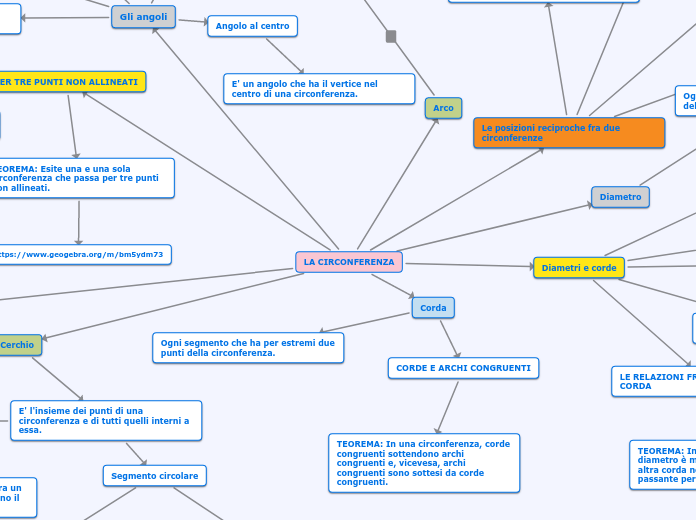
LA CIRCONFERENZA
Gli angoli
Il luogo dei punti dai quali un segmentovisto sotto un angolo dato
TEOREMA: Il luogo dei punti che vedono un dato segmento sotto un angolo retto è la circonferenza che ha quel segmento come diametro.
La proprietà degli angoli al centro
e alla circonferenza corrispondenti.
TEOREMA: Un angolo al centro è il doppio di un angolo alla circonferenza che insiste sullo stesso arco.
https://www.geogebra.org/m/mnq4cdax
https://www.geogebra.org/m/qys76bm6
La posizione reciproca fra due circonferenze e la distanza fra i loro centri
TEOREMA: Condizione necessaria e sufficiente affinché due circonferenze siano tangenti esternamente è che la distanza dei centri sia uguale alla somma dei raggi.
TEOREMA: Condizione necessaria e sufficiente affinché due circonferenze siano secanti è che la distanza dei centri sia minore della somma dei raggi e maggiore della loro differenza.
https://www.geogebra.org/m/nqt9p5eq
TEOREMA: Condizione necessaria e sufficiente affinché due circonferenze siano tangenti internamente è che la distanza dei centri sia uguale alla differenza dei raggi.
TEOREMA: Condizione necessaria e sufficiente affinché due circonferenze siano una interna all’altra è che la distanza dei centri sia minore della differenza dei raggi.
TEOREMA: Condizione necessaria e sufficiente affinché due circonferenze siano
esterne è che la distanza dei centri sia maggiore della somma dei raggi.
Angolo alla circonferenza
Un angolo alla circonferenza è un
angolo convesso che ha il vertice sul-
la circonferenza e i due lati secanti la
circonferenza stessa, oppure un lato
secante e l’altro tangente.
Angolo al centro
E' un angolo che ha il vertice nel centro di una circonferenza.
Le posizioni reciproche fra due circonferenze
UNA INTERNA ALL'ALTRA: Quando due circoferenze avendo raggi diversi, tutti i punti della circonferenza minore sono interni a quella maggiore.
ESTERNE: Quando due circonferenze non hanno punti in comune.
TANGENTI: Quando due circonferenze hanno un solo punto in comune.
SECANTI: Quando due circonferenza hanno due punti in comune.
LE CIRCONFERENZE E LE RETTE
Le posizioni reciproche fra retta e circonferenza
TEOREMA: Una retta e una circonferenza che si intersecano non possono avere più di due
punti in comune.
Retta esterna
TEOREMA: Rispetto a una circonferenza, una retta è esterna se e solo se la distanza dal centro è maggiore del raggio.
Una retta è esterna a una circonferenza se non ha punti in comune con essa.
Retta tangente
Le tangenti passanti per un punto esterno alla circonferenza
TEOREMA: Se da un punto P esterno a una circonferenza si conducono le due rette tangenti a essa, allora i segmenti di tangente, aventi ciascuno un estremo nel punto P e l’altro in un punto in comune con la circonferenza, sono congruenti.
https://www.geogebra.org/m/ugrhgx9j
TEOREMA: Se una retta è tangente a una circonferenza di centro O in un suo punto H, allora è perpendicolare al raggio OH.
TEOREMA INVERSO: Se una retta è perpendicolare al raggio di una circonferenza nel suo estremo H, allora è tangente in H alla circonferenza.
TEOREMA: Rispetto a una circonferenza, una retta è tangente se e solo se la distanza dal centro è uguale al raggio.
https://www.geogebra.org/m/pnpbqehg
Una retta è tangente a una circonferenza se ha un solo punto in comune con essa.
Retta secante
TEOREMA: Rispetto a una circonferenza, una retta è secante se e solo se la distanza dal centro è minore del raggio.
Una retta è secante una circonferenza se ha due punti in comune con essa.
Diametri e corde
LE CORDE NON CONGRUENTI E LE DISTANZE DAL CENTRO
TEOREMA: Se due corde di una circonferenza non sono congruenti, la corda maggiore ha distanza minore dal centro.
LE CORSE CONGRUENTI E LA DISTANZA DAL CENTRO
TEOREMA INVERSO: In una circonferenza, corde aventi la stessa distanza dal centro sono congruenti.
TEOREMA: In una circonferenza, corde congruenti hanno la stessa distanza dal centro.
IL DIAMETRO PER IL PUNTO MEDIO DI UNA CORDA
TEOREMA: Se il diametro di una circonferenza passa per il punto medio di una corda, che non sia un diametro, allora la corda e il diametro sono perpendicolari.
IL DIAMETRO PERPENDICOLARE A UNA CORDA
TOREMA: In una circonferenza, se un diametro e una corda sono perpendicolari, il diametro divide a metà la corda e l’angoal centro e l’arco che le corrispondono.
https://www.geogebra.org/m/q4xug2tf
LE RELAZIONI FRA DIAMETRO E CORDA
TEOREMA: In una circonferenza, ogni diametro è maggiore di qualunque altra corda non
passante per il centro.
PER TRE PUNTI NON ALLINEATI
TEOREMA: Esite una e una sola circonferenza che passa per tre punti non allineati.
https://www.geogebra.org/m/bm5ydm73
Arco
E' la parte di circonferenza compresa fra due soli punti.
Cerchio
E' l'insieme dei punti di una circonferenza e di tutti quelli interni a essa.
Segmento circolare
A due basi
E' la parte di cerchio compresa fra due
corde parallele.
A una base
E' la parte di cerchio compresa fra un
arco e la corda che lo sottende.
Il settore circolare
E' la parte di cerchio compresa fra un arco e i due raggi che congiungono il centro con gli estremi dell'arco.
Diametro
Ogni corda che passa per il centro della circonferenza.
Corda
CORDE E ARCHI CONGRUENTI
TEOREMA: In una circonferenza, corde congruenti sottendono archi congruenti e, vicevesa, archi congruenti sono sottesi da corde congruenti.
Ogni segmento che ha per estremi due punti della circonferenza.