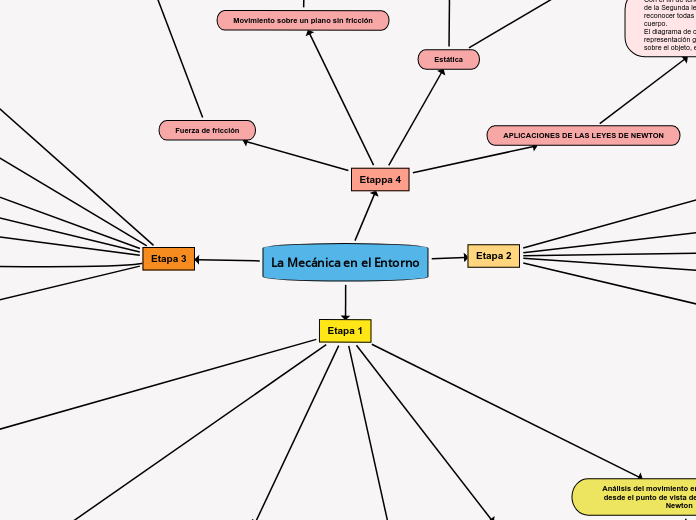
La Mecánica en el Entorno
Etappa 4
Fuerza de fricción
La fuerza de fricción f se opone al movimiento de deslizamiento entre las superficies en contacto y sigue una dirección paralela a ellas. Es decir, que la fuerza de fricción es proporcional a la fuerza de comprensión, y como vimos, esta comprensión es numéricamente igual a la fuerza normal. La fuerza de fricción aparece cuando hay movimiento o cuando un cuerpo se encuentra en reposo. además, depende de la naturaleza de las superficies en contacto y de la comprensión que las mantiene unidad.
Coeficiente de fricción estática
Sin objeto se le aplica una fuerza F y este no se mueve, se debe a la fuerza de fricción estática f s la cual se opone al movimiento del cuerpo. Es proporcionar a la comprensión, la cual es igual en magnitud a la fuerza normal (F N) ejercida por el plano sobre el objeto que se desliza sobre él.
Movimiento sobre un plano sin fricción
Para el análisis vectorial de las fuerzas y resolución de problemas necesitamos elaborar un diagrama de cuerpo libre: el procedimiento general en la elaboración de un diagrama de cuerpo libre es:
1. Identificar todas las fuerzas que actúan sobre el cuerpo y determinar si el movimiento es sobre el plano horizontal (eje x) o sobre el plano vertical (eje y).
2. Dibujar el diagrama de cuerpo libre con las fuerzas identificadas en el paso anterior.
3. Si existen fuerzas en algún otro cuadrante, se descomponen sus componentes rectangulares Fx y Fy.
4. Una vez elaborado el DCL (diagrama de cuerpo libre) establecemos la sumatoria de fuerzas en cada uno de los ejes.
5. La fuerza resultante de un conjunto de fuerzas aplicadas a un objeto la podemos encontrar mediante dos fórmulas:
• Utilizando la segunda ley de Newton: FR=ma
• Utilizando el método de las componentes: FR=√(Fx) ²+(Fy) ²
Estática
si sobre un objeto actúan dos o más fuerzas, estas producen una fuerza resultante. Si queremos que este objeto quede en equilibrio, se aplica una fuerza de igual magnitud, en la misma dirección y en sentido contrario a la resultante. A esta fuerza se le llama fuerza equilibrante.
Es la parte de la dinámica que se encarga de analizar el equilibrio de los cuerpos. Para que haya equilibrio se debe cumplir la:
Primera condición de equilibrio transnacional.
“Un cuerpo se encuentra en estado de equilibrio traslacional si y sólo una suma vectorial de las fuerzas que actúan sobre el es igual a cero”.
Cuando un cuerpo está en equilibrio, la resultante de todas las fuerzas que actúan sobre él es igual a cero.
son sistemas de fuerzas cuyas líneas de acción no se cruzan en el mismo punto.
se dice que dos o más fuerzas son concurrentes si sus líneas de acción se cruzan en el mismo punto.
son sistemas de fuerzas que actúan en diferentes planos, es decir, que actúan en el espacio de tres dimensiones.
son sistemas de fuerzas que se encuentran en el mismo plano
APLICACIONES DE LAS LEYES DE NEWTON
Con el fin de tener buenos resultados en la aplicación de la Segunda ley de Newton, tenemos que conocer y reconocer todas las fuerzas que actúan sobre un cuerpo.
El diagrama de cuerpo libre consiste en la representación gráfica, de todas las fuerzas que actúan sobre el objeto, en un sistema de coordenadas.
Etapa 3
Fuerza centrípeta
Su velocidad es buscando el centro. fuerza que se dirige al centro de rotación, su unidad de mediciones Newton ( N )
Fórmula: Fc= mac Fc=mv²/r
Fuerza centrípeta en función de velocidad angular, es igual a masa por radio por velocidad angular al cuadrado.
• En función de la velocidad tangencial y el radio de la circunferencia: ac= v ²/r F = m•ac F= m•v²/r
• En función a la velocidad angular y el radio de la circunferencia: ac=w ²r F= m•w²r
Fuerza y aceleración centrípeta
El movimiento circular se puede explicar desde el punto de vista de la primera y segunda ley de Newton. La primera ley de Newton establece que el movimiento natural de un cuerpo debe ser una línea recta y con velocidad constante, esto quiere decir que la velocidad no debe cambiar de magnitud ni dirección; sin embargo, en el movimiento circular, el objeto que gira a cambio de dirección constantemente, por lo que debe haber algo que provoque ese cambio
Por otra parte, la segunda ley de Newton establece que cuando un cuerpo no está en equilibrio, entonces está acelerado.
Aceleración centrípeta o radial
Esta aceleración apunta directamente hacia el centro del círculo, esta misma se encarga de producir un movimiento circular, y no un movimiento en forma recta, sus unidades son m/s.
Fórmulas: ac=v²/r ac= r w²
Frecuencia y periodo del movimiento circular
¿cómo se relaciona en una expresión matemática?, Si la frecuencia está dada en revoluciones/segundo, las revoluciones se convierten a radianes multiplicando por 2 π, entonces: (2π rad/1 rev) (N.rev./1 seg) = reg/s = w
W=2πf
Fórmula que describe la velocidad angular en términos de periodo y de frecuencia respectivamente, recordando que las unidades de la velocidad angular son rad/seg.
Velocidad tangencial (o lineal)
Su unidad de medida es m/s. todas las partes que contiene el objeto, mantienen una trayectoria perpendicular al radio al de esta circunferencia. Fórmula: V=r w
Frecuencia (f) y período (T)
• Frecuencia: número de ciclos (vueltas completas o revoluciones que efectúa un objeto por unidad de tiempo, su unidad de medida es revoluciones por segundo (rps). F=Núm. de revoluciones/tiempo.
• Período (T): tiempo que tarda un objeto en dar una vuelta completa, su unidad de medida es segundos (s). T= 1/f
Velocidad angular (w)
Magnitud (vectorial) desplazamiento angular dividido entre el tiempo que tardó en recorrer dicho ángulo. Sus unidades de medición son radianes por segundo (rad/seg)
Fórmula: w=∅/t
Donde: w=velocidad angular expresada en rad/seg.
∅ = desplazamiento angular en radianes.
T= tiempo expresado en segundos.
Desplazamiento angular
La instancia r se extiende desde el origen hasta el punto P (radio de un círculo) y el ángulo ∅ indica la amplitud entre el eje x y la línea r, que continuamente se miden en sentido ante horario a partir del eje x.
El desplazamiento angular es el valor del ángulo descrito por un cuerpo que se encuentra en movimiento circular, sus unidades de medida son los radianes.
Fórmula: ∅=S/R
En términos de descubrir el movimiento circular tangencialmente, se tiene que relacionar el desplazamiento angular con la longitud del círculo (s) es la distancia recorrida a lo largo de una trayectoria circular, nota que, si se suman todas las distancias s, se obtendrá la circunferencia.
Un radián se define como un ángulo formado en el centro de un círculo por un arco de circunferencia cuya longitud mide lo mismo que el radio del círculo. 1 radian= 57.3°
Cuando la longitud del arco de circunferencia “s” es igual al radio “r” del círculo, entonces el ángulo ∅ formado, es igual a un radian.
Movimiento circular
Es el que describe un cuerpo cuando se mueve alrededor de un centro de rotación.
Es decir, cuando gira alrededor de un punto fijo llamado eje de rotación o bien cuando su trayectoria es una circunferencia. Sólo tiene dos sentidos: a favor o en contra de las manecillas del reloj.
Etapa 2
Tiro vertical
Movimiento que describe un cuerpo cuando se lanza verticalmente hacia arriba o hacia abajo después moverse bajo la acción de la gravedad. Es gobernado por la acción de la fuerza gravitacional y de la aceleración que esta produce. podemos describir con las mismas ecuaciones de la cinemática que hemos utilizado, debemos tener en cuenta su carácter vectorial con el objetivo de realizar el análisis de manera consciente y obtener resultados congruentes con el sistema de referencia que hemos elegido.
Tiro parabólico
El estudio del tiro se simplifica recordando que este movimiento tiene lugar en dos dimensiones, es decir, tiene un movimiento horizontal, pues el proyectil se desplaza lateralmente hasta regresar a tierra, y simultáneamente se desplaza en el eje vertical, primero, elevándose hasta alcanzar la altura máxima y, enseguida, bajaste al mismo nivel desde donde se lanzó, u otro nivel diferente.
Dado que el proyectil se lanza a una velocidad inicial (vi), necesita obtener las componentes horizontal y vertical de ésta con:
• Vix: vicos∅ es la componente horizontal de la velocidad inicial.
• Viy: visen∅ es la componente vertical de la velocidad inicial.
Este movimiento, al igual que el horizontal, tiene velocidad horizontal constante, ya que en esa dirección no hay ningún agente externo que haga que una velocidad cambie.
Tiro horizontal
Movimiento de un cuerpo que es lanzado desde cierta altura, en dirección paralela a la superficie terrestre. Su trayectoria es el resultado de la combinación de dos movimientos independientes: un horizontal; en el que el cuerpo avanza hacia el frente con velocidad constante, y otro movimiento vertical, en el cual actúa la fuerza de la gravedad, es decir, suelo ciudad vertical va aumentando 9.8 m/s durante cada segundo de tiempo a medida que el objeto va descendiendo.
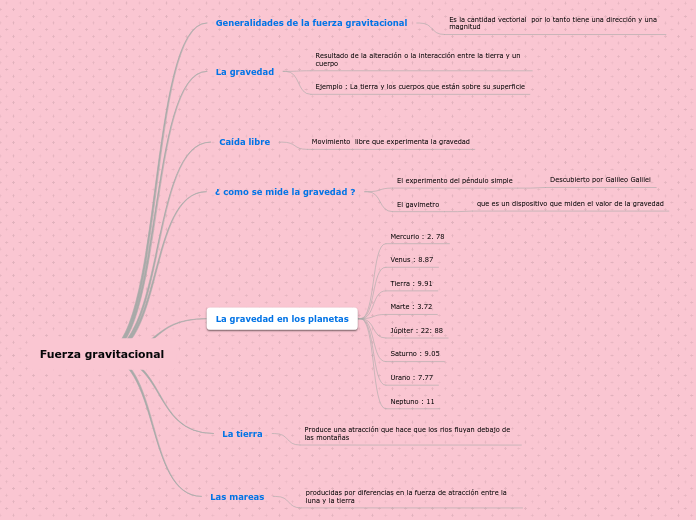
Caída libre
Movimiento que describe un cuerpo cuando se mueve libremente bajo la influencia de la gravedad. dicho movimiento tiene las siguientes características:
• Movimiento con trayectoria vertical rectilínea (hacia abajo).
• Movimiento con aceleración constante= -9.8 m/s² (tiene signo negativo ya que es un vector dirigido hacia el centro de la Tierra).
• Movimiento que parte del reposo (vi=0).
• Es un caso ideal, ya que se maneja bajo el supuesto de que la influencia del aire no afecta el desarrollo del movimiento.
• Aplicaremos las mismas ecuaciones del movimiento en una dimensión cambiando los símbolos las variables “x” del movimiento horizontal, por “y” para el movimiento vertical.
Recurriremos a la otra aportación de Galileo Galilei, conocida como “Principios de independencia de los movimientos”. Que establecen lo siguiente: “Cualquier movimiento en la naturaleza puede analizarse como la combinación de 2 o más movimientos rectilíneos independientes entre sí”.
Caída de los cuerpos
• Desmintió el dicho por Aristóteles con cálculos de la aceleración de la caída de los cuerpos.
• Caen a la misma velocidad sin importar el peso.
• El desplazamiento es una sola dirección que corresponde al eje vertical (eje “y”).
• Es un movimiento uniformemente acelerado y la aceleración que actúa sobre los cuerpos es la gravedad representada por la letra g.
Creía que al dejar caer cuerpos ligeros (de poco peso) y pesados desde una misma altura sus tiempos de caída serían diferentes. Él dijo “Los cuerpos más pesados llegaron al suelo antes que los ligeros”. Esta ciencia perduró por muchos años.
Etapa 1
Análisis del movimiento en una dimensión desde el punto de vista de las de leyes de Newton
Primera ley de Newton: “Todo cuerpo permanecerá en estado de reposo o de movimiento rectilíneo uniforme, a menos que una fuerza externa actúe sobre él”.
Segunda ley de Newton: “Cuando un cuerpo se encuentra bajo la acción de una fuerza neta no balanceada, la aceleración producida es directamente proporcional a la fuerza, e inversamente proporcional a la masa del cuerpo”.
Tercera ley de Newton: “A toda fuerza de acción, corresponde otra fuerza igual y contraria llamada reacción”.
¿Cómo relacionamos el estudio de la cinemática que hemos visto en el movimiento de una dimensión con las leyes de Newton?
“El vector velocidad de un objeto permanecerá constante, sí y sólo si la fuerza neta que actúa sobre él es igual a cero”.
Veamos ahora la relación con la segunda ley de Newton escribiéndola de esta otra manera:
“Cuando una fuerza neta diferente de cero actúa sobre un objeto, su velocidad cambia, es decir, el objeto está acelerado y esta aceleración es directamente proporcional a la fuerza neta e inversamente proporcional a la masa del mismo”.
Ecuaciones del movimiento rectilíneo
1. Ecuación de la posición: Xf=Xi+Vi t+1/2 at²
2. Ecuación de la velocidad: Vf=Vi+at
Debes desarrollar la capacidad de interpretar los datos con que cuentas y aplicar las ecuaciones anteriores de acuerdo con dichos datos. se pueden reconocer algunos comunes, a saber:
• Cuando el cuerpo parte del origen del sistema de coordenadas (Xi=0),
• Cuando el cuerpo parte del reposo, la velocidad inicial es cero (Vi=0),
• Cuando la velocidad es constante (a=0).
Movimiento en una dimensión
Movimiento en una dimensión
Al hablar de movimiento en una dimensión, nos referimos al movimiento que tiene un cuerpo cuando su trayectoria es una línea recta, movimiento rectilíneo.
Nos remitiremos, en el caso del movimiento acelerado, al análisis de situaciones con aceleración constante, ya sea en el plano horizontal o en el plano vertical.
Algunos autores hacen una distinción del movimiento rectilíneo en 2 tipos, a saber:
1. El movimiento rectilíneo uniforme, aquel en el que el cuerpo se mueve a velocidad y rapidez constantes; y
2. El movimiento rectilíneo uniforme acelerado, aquel en el que el cuerpo se mueve en línea recta con aceleración constante.
Método de las componentes para la suma de vectores
Existen varias formas de sumar vectores, por métodos gráficos como el del triángulo o el del polígono, métodos analíticos, nosotros nos enfocaremos a la descripción y a la aplicación del método analítico, denominado método de las componentes con el cual podría sumar cualquier cantidad de vectores.
Pasos del método de las siguientes componentes:
1. Transformar las coordenadas polares de cada uno de los vectores a coordenadas rectangulares, es decir, obtener con las siguientes fórmulas las componentes XY jet de cada uno de los vectores: Vx=v•cos∅ Vy=v•sen∅
Componentes polares de un vector (transformación de coordenadas rectangulares a polares)
En caso inversa transformar las coordenadas de un vector rectangular a polar, considera la utilización del Teorema de Pitágoras, el cual establece lo siguiente: “La suma de los cuadrados de los catetos de un triángulo rectángulo es igual al cuadrado de la hipotenusa”.
Catetos a los lados que forman el ángulo recto del triángulo; y el otro lado, que es el mayor de los tres, es la hipotenusa.
Formula: H²=C²+C²
Se le llama cateto adyacente al lado del triángulo que es parte de un triángulo formado por esta y la hipotenusa, y cateto opuesto al que se encuentra frente a dicho ángulo.
Magnitudes escalares y vectoriales
Las magnitudes físicas se pueden clasificar como escalares y vectoriales.
Magnitudes vectoriales: se precisan mediante un valor numérico, la unidad de medición correspondiente y además una dirección. Tenemos como ejemplos de magnitudes vectoriales la velocidad, el desplazamiento, la fuerza, el impulso y la aceleración
Características de las magnitudes vectoriales (vectores)
La dirección puede ser un punto cardinal ordinario (norte, sur, este, oeste y sus subdivisiones), o bien, puede describirse en términos de ángulos sexagesimales.
Cuando un vector se define de esta forma, se dice que está en su descripción de coordenadas polares. Otra forma de representar un vector es por medio de coordenadas rectangulares.
Magnitudes escalares: se precisan por completo mediante un valor numérico y una unidad de medida. estas no tienen dirección. Como ejemplos de magnitudes escalares tenemos la distancia, la rapidez, la masa, el tiempo y la temperatura.