Logicke funkcije

もっと見る

Osnove programiranja

Lucija Vukanovićにより

Bulova algebra

Amra Šabotićにより

Matematička logika

Isidora Lazićにより

Matematička logika

Marta Hutinecにより

Logicke funkcije

logička funkcija se može predstaviti:

Pomoću Karnoovih karti

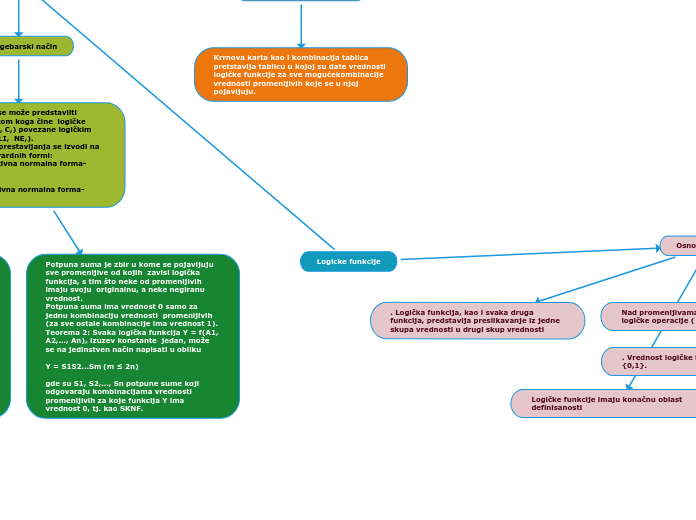
Krrnova karta kao i kombinacija tablica pretstavlja tablicu u kojoj su date vrednosti logičke funkcije za sve mogućekombinacije vrednosti promenljivih koje se u njoj pojavljuju.

Na algebarski način

Logička funkcija se može predstavliti algebarskim izrazom koga čine logičke promenljive (A, B, C,) povezane logičkim operacijama (I, ILI, NE,). Algebarski nacin prestavljanja se izvodi na dva nacina standrardnih formi: savršena disjunktivna normalna forma-suma proizvoda savršena konjuktivna normalna forma-proizvod suma

Potpuna suma je zbir u kome se pojavljuju sve promenljive od kojih zavisi logička funkcija, s tim što neke od promenljivih imaju svoju originalnu, a neke negiranu vrednost. Potpuna suma ima vrednost 0 samo za jednu kombinaciju vrednosti promenljivih (za sve ostale kombinacije ima vrednost 1). Teorema 2: Svaka logička funkcija Y = f(A1, A2,..., An), izuzev konstante jedan, može se na jedinstven način napisati u obliku Y = S1S2...Sm (m ≤ 2n) gde su S1, S2,..., Sn potpune sume koji odgovaraju kombinacijama vrednosti promenljivih za koje funkcija Y ima vrednost 0, tj. kao SKNF.

Potpuni proizvod je proizvod u kome se pojavljuju sve promenljive od kojih zavisi logička funkcija, s tim što neke od promenljivih imaju svoju originalnu, a neke negiranu vrednost. Potpuni proizvod ima vrednost 1 samo za jednu kombinaciju vrednosti promenljivih (za sve ostale kombinacije ima vrednost 0). Teorema 1: Svaka logička funkcija Y = f(A1, A2,..., An), izuzev konstante nula, može se na jedinstven način napisati u obliku Y = P1 + P2 + ... + Pm (m ≤ 2n) gde su P1, P2,..., Pn potpuni proizvodi koji odgovaraju kombinacijama vrednosti promenljivih za koje funkcija Y ima vrednost 1, tj. kao SDNF.

Kombinacionom tablicom

Kombinaciona tablica predstavlja tablicu gde se sa jedne strane nalaze sve moguće kombinacije vrednosti promenljivih, a sa druge strane vrednost funkcije za te vrednosti promenljivih.  Ovaj način predstavljanja nije pogodan ako je broj promenljivih veliki zato što je broj vrsta tablica jednak 2n , gde je n broj promenljivih logičke funkcije

Osnovne osobine

Logičke funkcije imaju konačnu oblast definisanosti

. Vrednost logičke funkcije pripada skupu {0,1}.

Logičke funkcije se mogu definisati nad proizvoljnim brojem promenjivih.

Nad promenljivama logičke funkcije se vrše logičke operacije ( I, ILI, NE, ...).

. Logička funkcija, kao i svaka druga funkcija, predstavlja preslikavanje iz jedne skupa vrednosti u drugi skup vrednosti