によって Maxzine Rossler 13年前.
420
もっと見る
Translation Symmetry
Kind of like wall paper if you cut out a piece and slid it over, and repeat it is a horizontal fashion.
Rotational Symmetry
When the object can be rotated and it still looks the same.
Reflection Symmetry
-When you fold an object/picture in half and it is the exact same on each side.
Cones and Cylinders
-Cones and Cylinders are not polyhedra because they are not composed of polygonal regions.
-Cones are pyramids with an infinate number of lateral faces. They have a base, a lateral surface, and an apex.
-Cylinders are prisms with an infinate number of lateral faces. They have two bases and a lateral surface
Pyramids: Have a base with an apex that is opposite, with lateral faces. They are named by the shape of their bases. They can also be right or oblique pryamids.
Right: When the pyramid is straight up and down.
Oblique: The pyramid has a slant.
Prisms: Havev two bases and lateral faces, they can also be right or oblique. The shape of the bases determine the name.
-The bases are congruent and parallel.
Polyhedra: Plural of polyhedron.
Polyhedron: Joining plane polygonal regions from edge to edge forms a surface. Each of the polygonal regions are called a face.
-The vertices and edges of the polygonal regions are also the vertices and edges of the polyhedron.
A Regular Polyhedron consists of:
-The surface is convex.
-The faces are congruent regualr polygonal regions.
-The same number of faces meet at each vertex of the polyhedron.
There are 5 regular polyhedra called the Plantonic Solids.
Cube 6 squares
Tetrahedron 4 equalateral triangles
Octahedron 8 equalateral triangles
Icosahedron 20 equalateral triangles
Dodecahedron 12 regular pentagons
Dihedral Angle: When two planes intersect each other there is an angle created between them.
Regular Polygons
-A polygon with all of its sides congruent is a equalateral polygon.
-A polygon with all of its angles congruent is called equalangular.
-A polygon that is both equalateral and equalangular is called a Regular Polygon.
Angle measure in a Regular n-gon
-Each interior angle has measure (n - 2)*180/n
-Each exterior angles has a measure 360/n
-Each central angle has measure 360/n
Interior Angle: Also the vertex angle, is formed by two adjacent sides of the polygon.
Central Angle: If formed by connecting the center of the poly go to two adjacent verticies of the polygon.
Exterior Angle: If formed by one side of the polygon and the extension of an adjacent side.
Regular Polygon Sides Central Interior Exterior
*Triangle 3 120 60 120
*Square 4 90 90 90
Pentagon 5 72 108 72
*Hexagon 6 60 120 60
Heptagon 7 51.4 128.6 51.4
Octagon 8 45 135 45
Decagon 10 36 144 36
*Indicates the shapes tesselate.
Tessellation
Tessellation: Any arrangement in which nonoverlapping figures are placed together to entirely cover a region.
Circles
Circle: Is a set of all points that are a fixed distance (radius) from a single point (center).
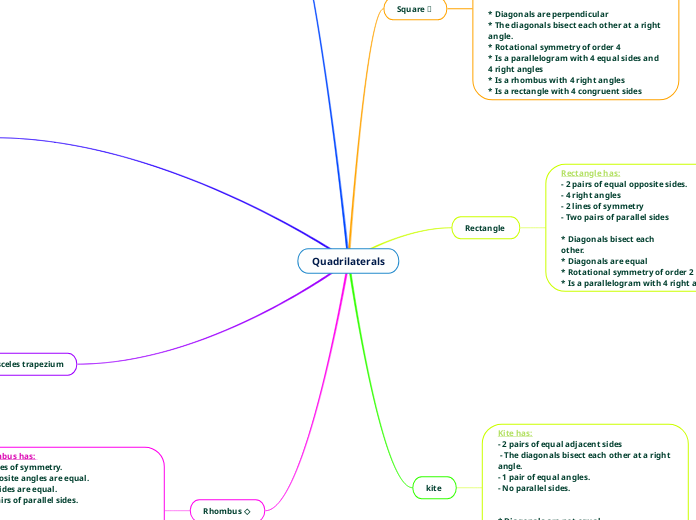
Quadrilaterals
Classification of Quadrilaterals:
Kite: A quadrilateral with two distinct pairs of congruent adjacent side. A kite can be either concave or convex.
Trapezoid: A quadrilateral that has exactly one pair of parallel sides.
Isosceles Trapezoid: A trapezoid with one pair of congruent angles with one of the parallel sides.
Parallelogram: A quadrilateral in which each pair of opposite sides is parallel.
Rhombus: A parallelogram with all of its sides the same length.
Rectangle: A parallelogram with a right angle.
Square: A rectangle with all sides of equal length and a right angle.
Triangles
Classification of Triangles:
Acute: A triangle is acute if all the angles are acute
Right: The triangle is a right triangle if one angle is a right angle.
Obtuse: A triangle is obtuse is an interior angle is obtuse.
Scalene: A triangle is scalene if no two sides have the same length.
Isosceles: A triangle is isosceles is at least two sides have the same length.
Equilateral: A triangle is equilateral is all three sides have the same length.
Curves: A collection of points that a pencil can trace without lifting until all the points in the set are covered.
-A curve is called simple if while tracing the curve, the pencil never touches a point more than once, which means the curve does not cross over itself.
-A curve is called closed if the pencil is lifted at the same point at which it started tracing.
-If a curve fulfills both of the descriptions then the curve is a simple, closed curve
Polygonal Curves: A curve that consists of a finitely many line segments.
-A polygon is a simple closed polygonal curve.
Jordan Curve Theorem
Sum of the Angle Measures in a Convex Polygon:
-The sum of the measures of the exterior angles of a convex polygon is 360 degrees
-The sum of the meausres of the interior angles of a convex n-gon is (n-2)180
-Only for convex polygons
Sum of Interior Angle Measures of a General Polygon:
-The sum of measures of the interior angles of any n-gon is (n-2)180
Perpendicular lines: are two lines that intersect at the right angels.
Complementary Angles: Are two angles that sum adds up to 90 degrees.
Supplementary Angles: Are two angles that sum adds up to 180 degrees.
Adjacent Angles: Two angles that have a common side and non overlapping interiors. (Share a common ray)
Vertical Angles: Are when a pair of non adjacent angles are formed by two intersecting lines. (Do not share a common side).
Corresponding Angles: When two lines are intersected by a transversal. Angles that are situated in similar positions are called corresponding angles.
*In special cases when we are given parellel lines then we are not only getting a pair or corresponding angles, but the angles in a given pair are congruent.
Corresponding Angles Property:
-If two parallel lines are cut by a transversal, then the corresponding angles have the same measure.
-If two lines in the plane are cut by a transversal and some pair of corresponding angles have the same measure then the lines are parallel.
-We are going to want to look at Alternate Interior angles.
Alternate Interior Angles: When two angles are created on the alternate sides of the transversal and interior to the lines.
Alternate Exterior Angles: When two angles are created on the alternate sides of the transversal and exterior to the lines.
Rays: a subset of a line that contains point P, called the endpoint of the ray, and all the points on the line lying to one side of P.
When you combine two rays that have a common end point, you get an Angle. this endpoint is called the vertex.
Midpoint: If D is a point on the line segment of AB and if D is the same distance from A as it is to B, then D is the midpoint of AB. Midpoint in the point in the middle.
Identifying Angles
Angles can be named by:
-Just using their vertex (only if it does not cause confusion).
-Three letter notation <BAC, where B and C are one each of the rays and A is their vertex.
-Named by other label such as <2
Zero Angle: m(<A = 0)
Acute Angle: 0 < m(<B)< 90
Right Angle: M(<C) = 90
Obtuse Angle: 90 < m(<D) < 180
Straight Angle: m(<E) = 180
Reflex Angle: 180 < m(<F) < 360
Any line can be viewed as a copy of the real number line. So when we discuss the distance between two points A and B on a line, we can view A as corresponding to the real number X1 and B corresponding to the real number X2. We can then define the distance from A to B to be the absolute value of the difference between X1 and X2:
l x1-x2 l
Congruent Line Segments- If two line segments have the same length they are said to be congruent.
Points: Have no dimension. They can be represented by dots when they are on paper.
Lines: Can be represented by the mark you leave from your writting utensil when drug along a straightedge. Any two points determine one and only one line that contains the two points.
Planes: A set of at least three points that idealize a flat space. Three non Collinear points determine a plane. Subsets (called plane figures or shapes) lie within the plane.
Parallel Lines
Parallel Lines- Two lines that do not have a point in common.
If two lines are not parallel they will have a point in common and that point is called their Intersection.
A line that intersects two other lines is called a Transversal.
Collinear Points
Collinearity- Two points on the same line.
Expected Value: P1 * V1 + P2 * V2...Pn * Vn.
P1 and P2...Pn are the probabilities of each outcome and V1 * V2...Vn are the values associated with each of the respective outcomes.
Example: There are 2 $1 bills, 3 $2 bills, and 1 $50 bill. Reach in and select one at random. It is $20 charge to play. What is the expected value? Is this fair?
Event Probability Value P*V
$1 2/6 1 2/6
$2 3/6 2 6/6
$50 1/6 50 50/6
Sum = $9.66
After you find the sum all the numbers in P*V you use that number and subtract how ever much money it was to begin with. which would be $20 in this case and you get:
$9.66
-$20.00
-$10.33
-$10.33 is the expected value of this problem. Since the number is so far away from 0 it would be unfair to play because the chances of you making more than you paid to play are slim.
P (A and then B) = P(A) * P(B) taking into consideration the effect event A may have on event B (Independent or Dependent events).
Independent Event: Is when the two events have no impact on eachother
Dependent Event: Is when one event influences the other event.
Example:
What is the probability of rolling a die and obtaining a 4 on the first roll and an even number on the second?
P(2,then even) = P(2) * P(even)
1/6 * 1/2 = 1/12
1/12 would be the P(2,then even)
When order does not matter. To figure out how many ways you can select x items/people from y items/people is-
C (y,x) = y!/(y!-x!) x!
Example:
C (5,2) = 5!/ (5-2)! 2! = 5!/2!3! = 5*4*3*2*1 = 5*4 = 10
2*1 3*2*1 2*1
3*2*1 cancles out on the top and bottom leaving 5*4 on the top and 2*1 on the bottom and that looks like
20 = 10
2
If ORDER MATTERS then to figure out how many ways you can select x items/people from y items/people is
P (y,x) = y!/(y-x)!
P (5,2) = 5!/(5-2)! = 5!/3! = 5*4*3*2*1 = 5*4 = 20
3*2*1
The 3*2*1 cancles out on the top and bottom to leave 5*4 on the top which leaves the answer to be 20.
0 < P(E) < 1
The probability is NEVER less than 0 or greater than 1.
Probability of Compound Events
An event that can be described using the intersection (and), union (or), or complement (not)of the other events is called a Compound Event.
Addition Property for unions/or
P(A U B)= P(A) + P(B) - P(A n B)
If A and B are mutually exclusive then P(A U B) = 0
Certain
If an event has a probability of 1 then the event is
Certain.
Impossible
If the event has a probability of 0 then the event is Impossible.
Theorical Probability:
In a theorical probability there is no experiment conducted. You use the "ideal" conditions.
For example:
What is the theoretical probability of rolling a 5?
5 is one number of a 6 sided dice therefore the answer would be 1/6.
Experimental Probability:
Is when you preform an experiment to determine the likelihood of the outcome. For example, you would actually flip a coin to get the results and then just use that as your probability.
If you were to conduect an experiment of flipping a coin 200 times. If you flip the coin and 125 times the coin lands on heads then your probability of getting heads would be 125/200.
Experiment- You do or change something. Such as rolling a dice, flipping a coin, or spinning a spinner.
Outcome- The different results of an experiment.
Sample Space- The set of all the outcomes in an experiment.
For example the sample space on a dice is 1,2,3,4,5,6.
Mutually Eclusive- When two events, event A and event B share nothing in common. They are disjoints that do not over lap and do not occur at the same time.
Example: Rolling a dice a flipping a coin.
Rolling and even number and rolling and odd
number.
Complementary Events- When event A is complementary of event B. Then P(A)+P(B)=1. These events do overlap and the two sets together must be the whole sample space.
Example: Drawing a black card and drawing a red card.
