によって Maye Romero 5年前.
969
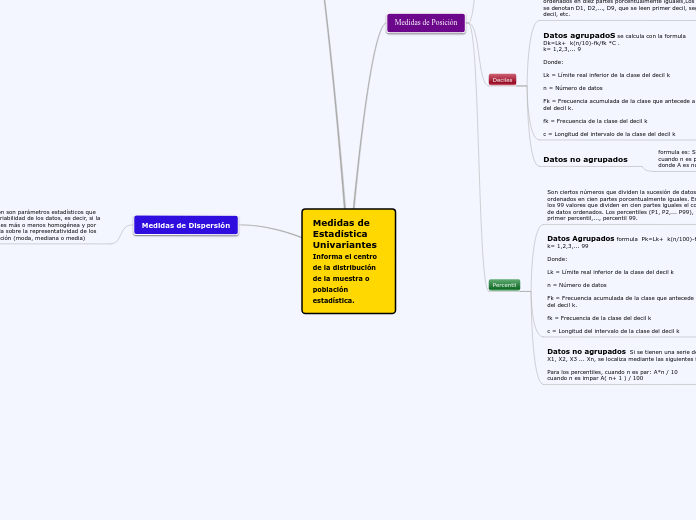
Medidas de Estadística Univariantes Informa el centro de la distribución de la muestra o población estadística.
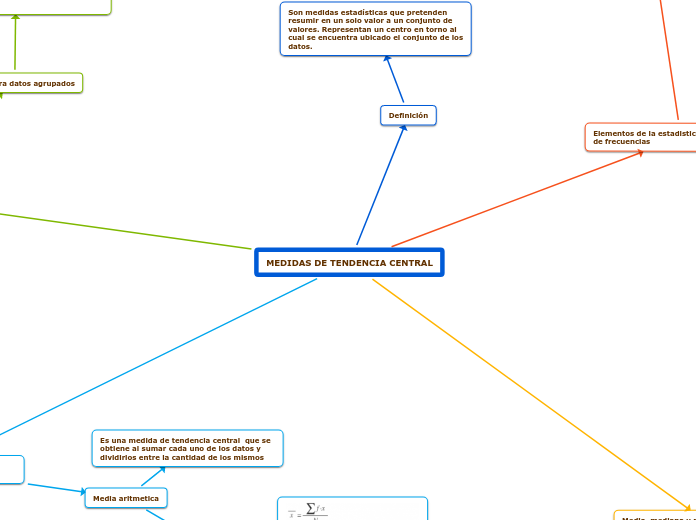
Las medidas de estadística univariantes son esenciales para describir la distribución de una muestra o población. Entre las medidas de tendencia central, se destacan la mediana, la moda y la media.