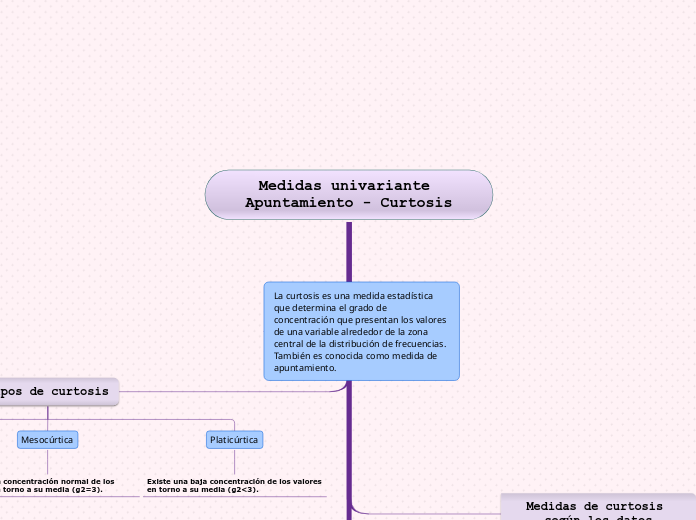
Medidas univariante Apuntamiento - Curtosis
La curtosis (o apuntamiento) es una medida de forma que mide cuán escarpada o achatada está una curva o distribución.
Este coeficiente indica la cantidad de datos que hay cercanos a la media, de manera que a mayor grado de curtosis, más escarpada (o apuntada) será la forma de la curva.
Tipos de curtosis
Platicúrtica
Existe una baja concentración de los valores en torno a su media (g2<3).
Mesocúrtica
Existe una concentración normal de los valores en torno a su media (g2=3).
Leptocúrtica
Existe una gran concentración de los valores en torno a su media (g2>3)
Exceso de curtosis
En algunos manuales la curtosis se presenta como exceso de curtosis. En este caso esta se compara directamente con la de la distribución normal. Dado que la distribución normal tiene curtosis 3, para obtener el exceso, solo habría restarle 3 a nuestro resultado. Exceso de curtosis = g2-3 = 3,34-3 = 0,34.
La interpretación del resultado en este caso, sería la siguiente:
g2-3 > 0 -> distribución leptocúrtica.
g2-3 = 0 -> distribución mesocúrtica (o normal).
g2-3 < 0 -> distribución platicúrtica.
Medidas de curtosis según los datos
Datos agrupados en intervalos
Datos agrupados en tablas de frecuencias
Datos sin agrupar
La curtosis es una medida estadística que determina el grado de concentración que presentan los valores de una variable alrededor de la zona central de la distribución de frecuencias. También es conocida como medida de apuntamiento.
