によって Jessica Williams 12年前.
2993
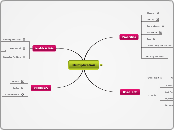
Multiplication Mind-Map
The information is structured to help elementary school students grasp the concept of multiplication. It covers essential terminology, including the definition of a product and factors.
によって Jessica Williams 12年前.
2993

もっと見る
The goal of this map is to organize the information needed to introduce multiplication to elementary school students.
Factors are the numbers you multiply together to get the product (answer).
A product is the answer when two or more numbers are multiplied together.
Repeated addition is just what it sounds like. An example of using repeated addition for the multiplication problem 4 X 5 would be 5+5+5+5. Teaching repeated addition to students is a way for the students to grasp the underlying concept of what multiplication really is.
In the area model of multiplication the two numbers that are being multiplied represent the dimensions (length and width) of a rectangle. When the dimensions are multiplied, the result is the area of the rectangle.
This is a method of modeling multiplication by joining a certain number of equivalent sets. Sets are arranged in equal rows and columns. The arrangement of these sets is referred to as a rectangular array. One number represents the number of sets (rows) and the other number represents the number of objects in each set (row).
The sum of two numbers multiplied by a third number is equal to the sum of each addend multiplied by the third number.
Example:
a(b+c) = (ab) + (ac)
The zero property states that whenever zero is a factor in a multiplication problem, the product will always be zero.
The associative property states that, when multiplying 3 or more numbers, the product will remain the same regardless of the grouping of the numbers.
Example:
(ab)c = a(bc)
The commutative property states that changing the order of the factors in a multiplication problem will not change the product.
The identity property of multiplication states that when any real number (we will say "r") is multiplied by 1, the real number is always the answer. r X 1 is ALWAYS r.
The closure property states that the product of any two real numbers equals another real number.