Pre- Calculus CHAPTERS 6-8

もっと見る

Calculus

Saloni Todiにより

Trigonometric Functions and Identities

Caterina Calabrettaにより

Affter Effects

Winder Echaccaya Huamanにより

R-formula and Trigonometry(Sean Group)

Sean Leowにより

Pre- Calculus CHAPTERS 6-8

CHAPTER 8: Applications of Trigonometric Functions

Simple Harmonic Motion; Damped Motion

Analyze the Harmonic Motion

Analyze the Damped Motion

Graph the Sum of Two Functions

Build a Model for an Object in Simple Harmonic Motion

Area of a Triangle

The area N of a triangle is N=1/2 bh

Solve for the Area of SSS Traingfles

Solve for the Area of SAS Triangles

The Law of Cosines

The square of one side of a triangle is equal to the sum of the squares of the two other sides and subtract twice their product times the cosine of their angle that is included

Solve Applied Problems

Solve SSS Triangles

Solve SAS Trangles

The Law of Sines

If none of the angles of a triangle is a right triangle it is called oblique

Solve to Applied Problems

Solve SSA Triangles

Solve SAA or ASA Triangles

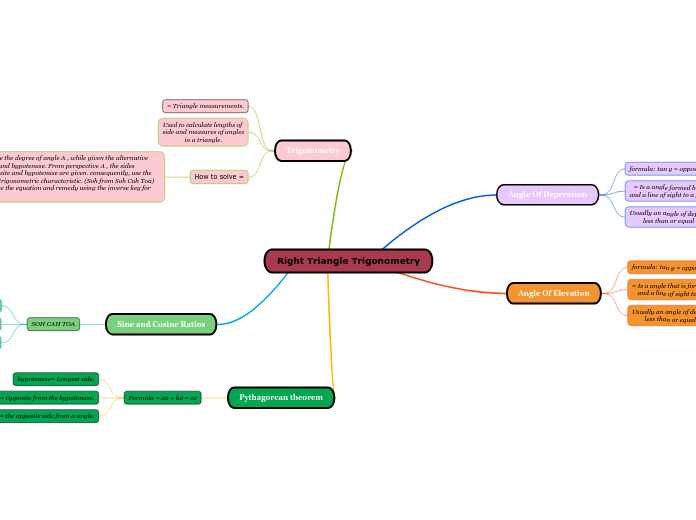
Right Triangle Trigonometry; Applications

A triangle is one angle that has a right angle (90 degrees)

The opposite side of the right angle is called the hypotenuse

CHAPTER 7: Analytic Trigonometry

Product-to-Sum and Sum-to-Product Formulas

Express Products as Sums

Express Sums as Products

Use the derive formulas for writing the products of sines or cosines as sums or differences

Double- angle and half-angle Formulas

Double- Angle Formulas to find Exact Values

Find Exact Values

Find Established Identities

In order to find the formulas use:

Sum and Difference Formulas

Use the Unit Circle to find the formulas

The derivation of trigonometric identities by obtaining formulas involves the sum or the difference of two angles

Trigonometric Identities

For every value of x both of the functions are defined

Identically Equal, Identity, and Conditional Equations

Two functions f and g are identically equal

f(x)=g(x)

Trigonometric Equations

Solving Equations by a Single Trigonometric Function

Using a Graphing Utility

Fundamental Identities

Quadratic in Form

Using a calculator

The Inverse Trigonometric Functions

Define the Inverse Secant, Cosecant, and Cotangent Functions

Most calculators do not have the keys to find the inverse cotangent, cosecant, or secant function

Evaluate them by converting the inverse trigonometric functions

The Inverse Sine, Cosine, and Tangent Functions

Define the Inverse Sine Function and the horizontal line y=b and where b is between the -1 and 1

Intersects the graph of y=sin x infinitely many times for the horizontal line test

CHAPTER 6: Trigonometric Functions

Key Terms

Angle in Standard Position: Vertex is at the origin

1 Degree = 1/ 360 revolution

1 Radian= The measure of a central angle of a circle and the length is equal to the radius of the circle.

Unit Circle= A circle with the radius of 1 unit, and the centered origin of the coordinate plane.

sine (sin)= length of the side opposite the angle to the length of the hypotenuse

cosine (cos)= an angle in a right triangle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse

tangent (tan)= ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.

cosecant (csc) = csc(0)=1/sin(0)

secant (sec)= sec(0)-1/cos(0)

cotangent(cot)= cot(0)=1/tan(0)

MAIN KEYS

Angles, Arc Length, and Circular Motion

Find the Linear Speed of an Object

Distinguish the linear speed v of the object

w= 0/t

v= s/t

Find the Area of a Sector of a Circle

0 measured in radians, is a central angle of this circle.

consider a circles of a radius r and two central angles

Theorem Area of a Sector

The area A of the sector of a circle of radius r formed by a central angle of 0 radians

Convert from the Degrees to Radians and from Radians to Degrees

Subdivisions of a degree may be obtained by the use of decimals, the notion of minutes and seconds

One minute , is 1/60 degree

One second, 1/3600 degree

1 counterclockwise revolution= 360 degrees

Angles and Degree Measure

The angle is formed by the rotating initial side that is exactly once in the counterclockwise and direction to = 1 revolution

One degree, is 1/360 revolution

Convert between Decimal and Degree, Minute, Second that Measures for Angles

When a ray, or half-line is a portion of a line that starts at a point V on the line and extends the indefinity in 1 direction

When two rays are drawn into the common vertex they form a ray of angle for the initial side

An angle 0 = standard position for the vertex at the origin of the rectangular coordinate system and the initial side for the coincides and positive x-axis