FUENTES CONSULTADAS
¿Cuáles son las fuentes de las que se obtendrán los datos?
Según Córdova (2003), es el valor que divide en dos partes iguales a un conjunto de datos ya ordenados. La mediana no se ve afectada por los valores extremos, de
manera que puede utilizarse cuando están presentes.
Según Córdova (2003), es el valor del conjunto de datos que aparece con mayor
frecuencia. A diferencia de la media, los valores extremos no afectan a la moda. Con
frecuencia, hay una moda o hay casos en que presentan varias modas.
Según Córdova (2003), la media aritmética (por lo general se llama la media), es la medida más común en la que todos los valores desempeñan el mismo papel, sirve como un punto de equilibrio del conjunto de datos. Se calcula sumando todos los valores del conjunto de datos y dividiendo el resultado por el número de la muestra.
La mediana (Me)
La moda (Mo)
La media o media aritmética
Las medidas de tendencia central son las medidas que describen cómo todos los valores de los datos se agrupan en torno a un valor central.
Hernández (2014), afirma que <>.
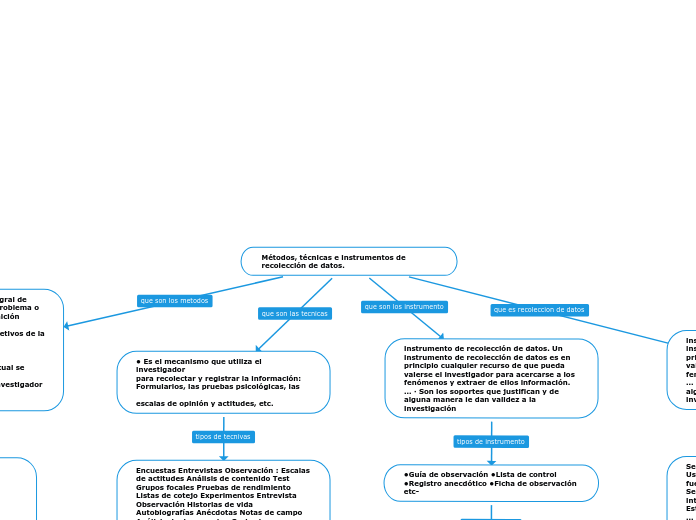
El cuestionario
¿En dónde se localizan tales fuentes?
¿A través de qué medio o método vamos a recolectar los datos?
Según Nortes (1987), es un conjunto
de preguntas sobre los hechos o aspectos que interesan en un investigación y que son contestadas por los encuestados.
Escala para medir actitudes
¿De qué tipos de instrumentos de recolección de datos disponemos?
Planteamiento del problema. Planificación. Recojo de datos. Análisis. Interpretación.
Conclusión. Reporte de los resultados.
¿Qué implica esta etapa?
Estrategias y técnicas para recopilar y procesar datos
Fases
Hernández, (2014), nos dice que, «recolectar los datos implica elaborar un plan detallado de procedimientos que nos conduzcan a reunir datos con un propósito específico. Este plan incluye determinar:
¿De qué forma vamos a prepararlos para que puedan analizarse y respondamos al planteamiento del problema?
TÉCNICA DE MUESTREO Y MEDIDAS ESTADÍSTICAS
Técnicas de muestreo
Muestreo No probabilístico no probabilístico no todos los miembros de la población tienen la oportunidad de participar en el estudio.
Muestreo Probabilístico. Todos los individuos tienen la misma probabilidad de ser elegidos para formar parte de una muestra.
Muestreo aleatorio por conglomerados
Muestreo aleatorio estratifico
Muestreo aleatorio sistemático
Muestreo Aleatorio simple: todos los elementos que forman el universo - y que por lo tanto están incluídos en el marco muestral - tienen idéntica probabilidad de ser seleccionados para la muestra.
AXIOMAS Y PROPIEDADES DE LA PROBABILIDAD
Axioma 3
La probabilidad de unión de eventos mutuamente excluyentes es igual a la suma de las probabilidades de cada evento individual.
Axioma 2
La probabilidad de que en el experimento se obtenga algún resultado, cualquiera que sea, es 1.
Axioma 1
Dado un experimento, la probabilidad de que ocurra un evento cualquiera (E) debe ser un número real no negativo
CÁLCULO DE PROBABILIDADES
Métodos comunes para encontrar la probabilidad de un evento
3. Probabilidad condicional: Para dos eventos cualesquiera A y B con P(B) > 0, la probabilidad condicional de A dado que B ha ocurrido está definida por:
P(A/B) = P(A∩B)/P(B)
2. Permutaciones y Combinaciones
Un subconjunto ordenado se llama permutación. El número de permutaciones de tamaño k que se puede formar con los n individuos u objetos en un grupo será denotado con Pk,n. Un subconjunto no ordenado se llama combinación. Una forma de denotar el número de combinaciones es Ck,n, pero en su lugar se utilizará una notación bastante común en los libros sobre probabilidad: (nk), que se lee así: “de n se elige k” (Devore, 2019).
Regla de conteo para permutaciones el número de formas en que podemos acomodar n objetos distintos tomándolos una cantidad r a la vez, es:
(1+𝑥)𝑛=1+𝑛𝑥/1!
1. Aproximación de la probabilidad por frecuencias relativas
Realice (u observe) un procedimiento y cuente el número de veces que ocurre el evento
A. Entonces, P(A) se aproxima de la siguiente manera:
P(A) = número de veces que ocurrió A/número de veces que ocurrió el procedimiento
Si un procedimiento tiene n eventos simples diferentes que son igualmente probables, y si el evento A puede ocurrir de s diferentes maneras, entonces
P(A) = número de veces en que ocurre A/número de eventos simples diferentes.
s/n
Diagramas de árbol: Se utilizan para determinar el espacio muestral, se pueden descomponer en varias fases y que ofrecen un número finito de posibilidades en cada paso. Por otro lado, aunque a veces la propia construcción del diagrama de árbol ayuda a comprender la estructura del experimento y, por tanto, a resolver los problemas, su utilidad es aún mayor en el cálculo de probabilidades en el contexto de un experimento compuesto (Roldán, 2018).
TIPOS DE ESPACIOS MUESTRALES
Espacio muestral continuo: Un espacio muestral es continuo cuando el número de posibles resultados es infinito.
El peso de un individuo de un grupo, que puede ser cualquier número real positivo (Tomado de ProbabilidadyEstadística.net, s.f.).
Espacio muestral discreto (o numerable): Un espacio muestral es discreto cuando el número de posibles resultados es finito o infinito numerable.
El lanzamiento de un dado y el lanzamiento de una moneda tienen espacios muestrales discretos finitos. Pero lanzar una moneda hasta que salga cara consiste en un espacio muestral discreto infinito numerable, porque el número de resultados es finito pero el número de lanzamientos no, ya que no sabes cuántas veces debes tirar la moneda hasta que salga cara.
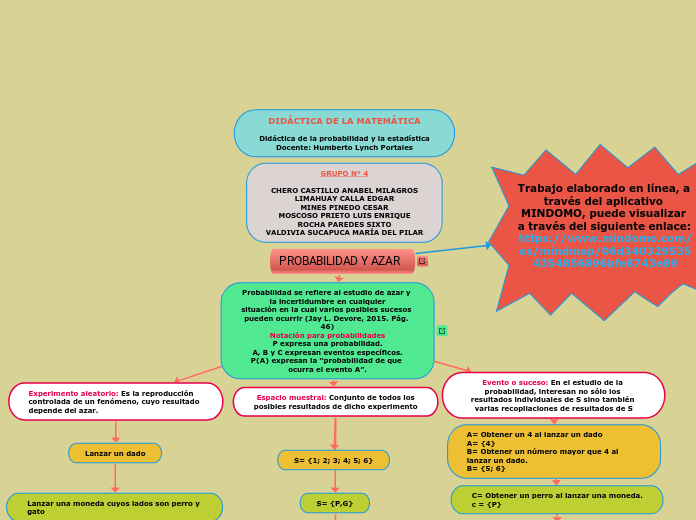
DIDÁCTICA DE LA MATEMÁTICA
Didáctica de la probabilidad y la estadística
Docente: Humberto Lynch Portales
GRUPO N° 4
CHERO CASTILLO ANABEL MILAGROS
LIMAHUAY CALLA EDGAR
MINES PINEDO CESAR
MOSCOSO PRIETO LUIS ENRIQUE
ROCHA PAREDES SIXTO
VALDIVIA SUCAPUCA MARÍA DEL PILAR
TIPOS DE EVENTOS
Evento simple: Es un resultado o un evento que no se puede descomponer en componentes más simples
Evento compuesto: Es cualquier evento que combina dos o más eventos simples.
PROBABILIDAD Y AZAR
Trabajo elaborado en línea, a través del aplicativo MINDOMO, puede visualizar a través del siguiente enlace: https://www.mindomo.com/es/mindmap/06d3403295354354856896bfe8743e89
Probabilidad se refiere al estudio de azar y la incertidumbre en cualquier
situación en la cual varios posibles sucesos pueden ocurrir (Jay L. Devore, 2015. Pág. 46)
Notación para probabilidades
P expresa una probabilidad.
A, B y C expresan eventos específicos.
P(A) expresan la “probabilidad de que ocurra el evento A”.
Experimento aleatorio: Es la reproducción controlada de un fenómeno, cuyo resultado depende del azar.
Lanzar un dado
Lanzar una moneda cuyos lados son perro y gato
Lanzar dos dados
Un nacimiento
Tres nacimientos
Evento o suceso: En el estudio de la probabilidad, interesan no sólo los resultados individuales de S sino también varias recopilaciones de resultados de S
D = Obtener al menos un gato al lanzar dos monedas.
D = S= {(P,G), (G,P), (G,G)}
E = Que naciera 1 mujer (evento simple).
F = Que naciera 2 mujeres y 1 hombre
F = S= {(H,M,M), (M,M,H), (M,H,M)}
A= Obtener un 4 al lanzar un dado
A= {4}
B= Obtener un número mayor que 4 al lanzar un dado.
B= {5; 6}
C= Obtener un perro al lanzar una moneda.
c = {P}
Espacio muestral: Conjunto de todos los
posibles resultados de dicho experimento
S= {P,G}
S= {(P,P), (P,G), (G,P), (G,G)}
S= {H,M}
S= {(H,H,H), (H,H,M), (H,M,M), (M,M,M), (M,M,H), (M,H,H), (H,M,H), (M,H,M)}
S= {1; 2; 3; 4; 5; 6}