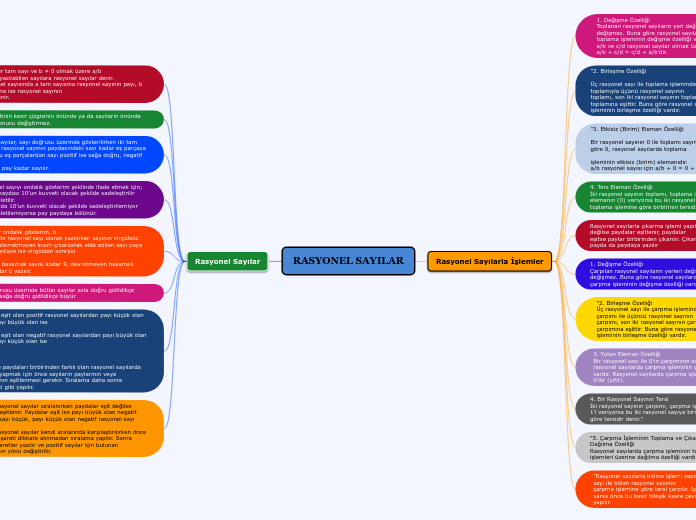
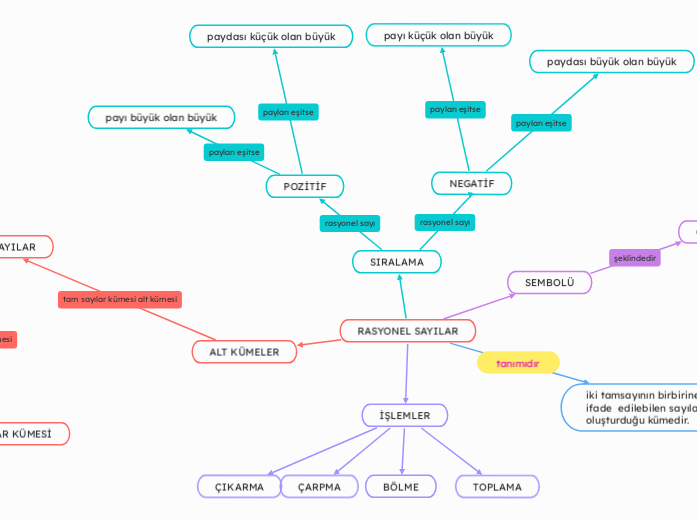
RASYONEL SAYILAR
Conflict is present everywhere in the world around us. We experience conflict on a daily basis, and it can be minor or major.
Conflict in a story is a struggle between opposing forces. Characters must act to confront those forces and there is where conflict is born. If there is nothing to overcome, there is no story. Conflict in a story creates and drives the plot forward.
Rasyonel Sayılar
Negatif rasyonel sayılar sıralanırken paydalar eşit değilse paydalar eşitlenir. Paydalar eşit ise payı büyük olan negatif rasyonel sayı küçük, payı küçük olan negatif rasyonel sayı büyüktür.
Negatif rasyonel sayılar kendi aralarında karşılaştırılırken önce sayıların işareti dikkate alınmadan sıralama yapılır. Sonra negatif işaretler yazılır ve pozitif sayılar için bulunan sıralamanın yönü değiştirilir.
Paydaları eşit olan pozitif rasyonel sayılardan payı küçük olan küçük, payı büyük olan ise
büyüktür.
Paydaları eşit olan negatif rasyonel sayılardan payı büyük olan küçük, payı küçük olan ise
büyüktür.
Payları ve paydaları birbirinden farklı olan rasyonel sayılarda sıralama yapmak için önce sayıların paylarının veya paydalarının eşitlenmesi gerekir. Sıralama daha sonra yukarıdaki gibi yapılır.
Sayı doğrusu üzerinde bütün sayılar sola doğru gidildikçe küçülür, sağa doğru gidildikçe büyür
Devirli bir ondalık gösterim, b
a biçiminde rasyonel sayı olarak yazılırken sayının virgülsüz
hâlinden devretmeyen kısım çıkarılarak elde edilen sayı paya yazılır. Paydaya ise virgülden sonraki
devreden basamak sayısı kadar 9, devretmeyen basamak sayısı kadar 0 yazılır.
Bir rasyonel sayıyı ondalık gösterim şeklinde ifade etmek için;
• Sayının paydası 10’un kuvveti olacak şekilde sadeleştirilir veya genişletilir.
• Eğer payda 10’un kuvveti olacak şekilde sadeleştirilemiyor veya genişletilemiyorsa pay paydaya bölünür.
Rasyonel sayılar, sayı doğrusu üzerinde gösterilirken iki tam sayı arası, rasyonel sayının paydasındaki sayı kadar eş parçaya bölünür. Bu eş parçalardan sayı pozitif ise sağa doğru, negatif ise
sola doğru pay kadar sayılır.
“–” işaretinin kesir çizgisinin önünde ya da sayıların önünde olması sonucu değiştirmez.
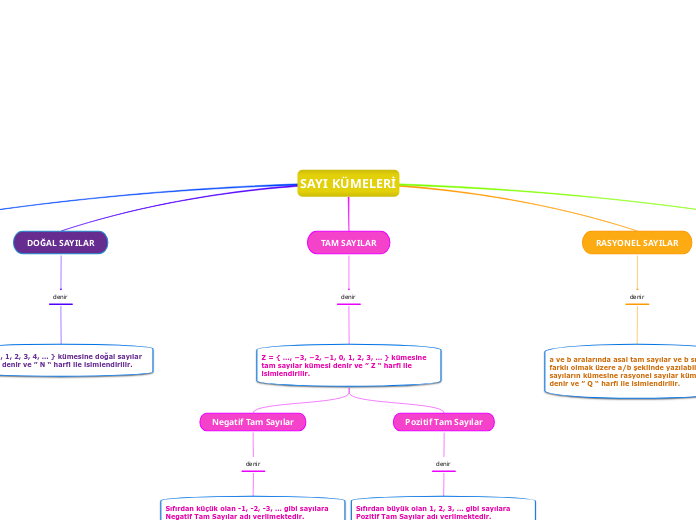
a ve b birer tam sayı ve b ≠ 0 olmak üzere a/b
biçiminde yazılabilen sayılara rasyonel sayılar denir.
a/b rasyonel sayısında a tam sayısına rasyonel sayının payı, b tam sayısına ise rasyonel sayının
paydası denir.
Rasyonel Sayılarla İşlemler
"Rasyonel sayılarla bölme işlemi yapılırken bölünen rasyonel sayı ile bölen rasyonel sayının
çarpma işlemine göre tersi çarpılır. İşlemde tam sayılı kesir varsa önce bu kesir bileşik kesre çevrilir, sonra bölme işlemi yapılır.
"5. Çarpma İşleminin Toplama ve Çıkarma İşlemleri Üzerine Dağılma Özelliği
Rasyonel sayılarda çarpma işleminin toplama ve çıkarma işlemleri üzerine dağılma özelliği vardır
4. Bir Rasyonel Sayının Tersi
İki rasyonel sayının çarpımı, çarpma işleminin etkisiz elemanı 1’i veriyorsa bu iki rasyonel sayıya birinin çarpma işlemine göre tersidir denir."
3. Yutan Eleman Özelliği
Bir rasyonel sayı ile 0'ın çarpımının sonucu 0’dır. Buna göre rasyonel sayılarda çarpma işleminin yutan eleman özelliği vardır. Rasyonel sayılarda çarpma işlemine göre yutan eleman 0’dır (sıfır).
"2. Birleşme Özelliği
Üç rasyonel sayı ile çarpma işleminde ilk iki rasyonel sayının çarpımı ile üçüncü rasyonel sayının
çarpımı, son iki rasyonel sayının çarpımıyla ilk rasyonel sayının çarpımına eşittir. Buna göre rasyonel sayılarda çarpma işleminin birleşme özelliği vardır.
1. Değişme Özelliği
Çarpılan rasyonel sayıların yerleri değiştirildiğinde çarpım değişmez. Buna göre rasyonel sayılarda
çarpma işleminin değişme özelliği vardır.
Rasyonel sayılarla çıkarma işlemi yapılırken paydalar eşit değilse paydalar eşitlenir, paydalar
eşitse paylar birbirinden çıkarılır. Çıkan sonuç paya, ortak payda da paydaya yazılır
4. Ters Eleman Özelliği
İki rasyonel sayının toplamı, toplama işleminin etkisiz elemanın (0) veriyorsa bu iki rasyonel sayı
toplama işlemine göre birbirinin tersidir.
"3. Etkisiz (Birim) Eleman Özelliği
Bir rasyonel sayının 0 ile toplamı sayının kendisine eşittir. Buna göre 0, rasyonel sayılarda toplama
işleminin etkisiz (birim) elemanıdır. a/b rasyonel sayısı için a/b + 0 = 0 + a/b = a/b
"2. Birleşme Özelliği
Üç rasyonel sayı ile toplama işleminde ilk iki rasyonel sayının toplamıyla üçünü rasyonel sayının
toplamı, son iki rasyonel sayının toplamıyla ilk rasyonel sayının toplamına eşittir. Buna göre rasyonel sayılarda toplama işleminin birleşme özelliği vardır.
1. Değişme Özelliği
Toplanan rasyonel sayıların yeri değiştirildiğinde toplam değişmez. Buna göre rasyonel sayılarda
toplama işleminin değişme özelliği vardır. a/b ve c/d rasyonel sayılar olmak üzere; a/b + c/d = c/d + a/b'dir.