によって Carlos Martelo 4年前.
901
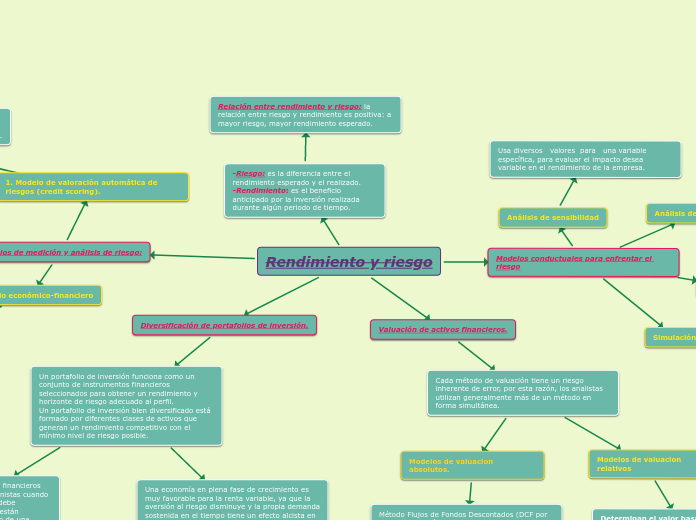
Simulación - Modelo - Montecarlo
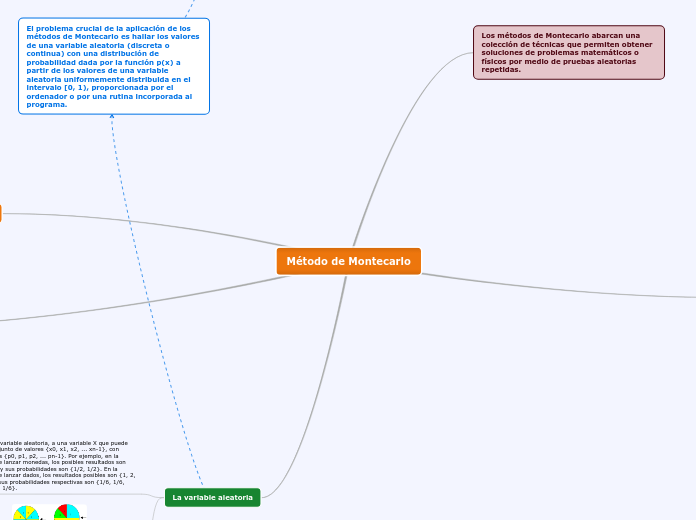
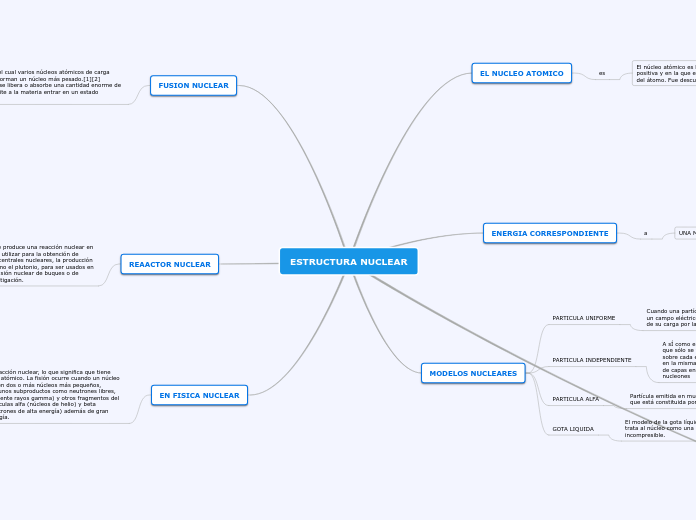
El método de Montecarlo se basa en técnicas que resuelven problemas matemáticos y físicos mediante pruebas aleatorias repetidas. La simulación es una herramienta clave en este método, utilizada por primera vez en 1949 por John Von Neumann y Stanislaw Ulam.