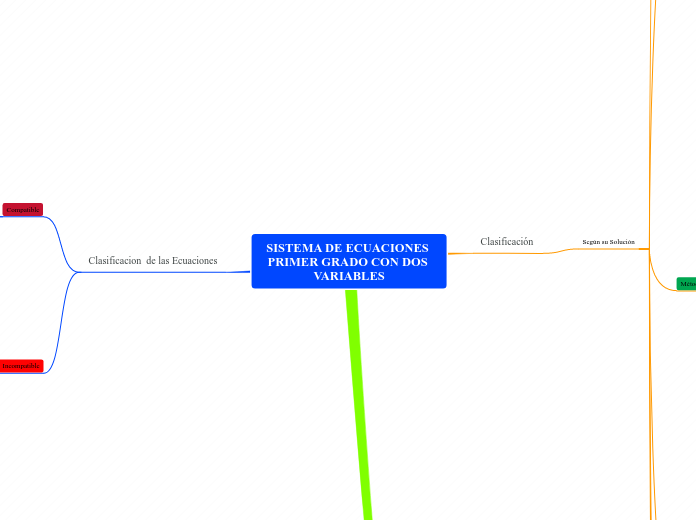
SISTEMA DE ECUACIONES PRIMER GRADO CON DOS VARIABLES
Clasificacion de las Ecuaciones
Incompatible
No llegan a tener solución
Compatible
Indeterminada
Tiene Infinitas soluciones
Determinada
Tiene un número determinado de soluciones
Revisa Más información en Classroom
Mi Classrom
Clasificación
Según su Solución
Otros heurísticos
Existen más métodos de resolución de ecuaciones: Método de Evaluación. Método de Ecuaciones diofánticas
Método Gráfico
Los pasos para resolver un sistema de ecuaciones por el método gráfico son los siguientes:
Despejamos la incógnita «y» en cada una de las ecuaciones
Representamos cada una de las rectas en los ejes de coordenadas
Las coordenadas del punto de corte de ambas rectas, será la solución del sistema de ecuaciones.
Método de las Determinantes
El Método de determinantes es una forma de resolución de sistemas de ecuaciones lineales, al igual que los métodos sustitución e igualación, este método permite obtener el resultado de un sistema de ecuaciones en unos simples pasos.
Método de Reducción ó Método de Eliminación
1. Elegimos una incógnita para eliminar en las ecuaciones. 2. Evaluamos los coeficientes de la variable seleccionada y con el MCM buscamos que ambas tengan coeficientes opuestos. 3. Multiplicamos a una o ambas ecuaciones con el objeto de que el variable elegida tenga coeficientes opuestos. 4. Sumamos o restamos ambas ecuaciones donde se elimina una de las variables. 5. resolvemos la ecuación de primer grado que queda. 6. Calculamos la otra incógnita sustituyendo. Sustituimos el valor de la incógnita y en alguna de las expresiones calculadas anteriormente.
Método de Sustitución
1. Elegimos una incógnita para despejar en una de las ecuaciones. 2. Despejamos la variable en una de las ecuaciones de nuestro sistema. 3. Sustituimos la ecuación en la ecuación que no despejamos despejadas. 4. Resolvemos la ecuación de primer grado obtenida: 5. Calculamos la otra incógnita sustituyendo. Sustituimos el valor de la incógnita y en alguna de las expresiones calculadas anteriormente.
Método de Igualación
Subtopic
1. Elegimos una incógnita para despejar en las dos ecuaciones. 2. Despejamos la variable en ambas ecuaciones de nuestro sistema. 3. Igualamos ambas ecuaciones despejadas. 4. Resolvemos la ecuación de primer grado obtenida: 5. Calculamos la otra incógnita sustituyendo. Sustituimos el valor de la incógnita y en alguna de las expresiones calculadas anteriormente.