Sistemas de ecuaciones

もっと見る

La convivencia y valores

Diego Parodiにより

AMBIENTE DE LA ORGANIZACION

Pero Gruyoにより

Familia, escuela y sociedad en la formación de valores éticos y morales

Karina Sánchezにより

Mapa mental valores y proyecto de vida

Hector Valdez Lunaにより

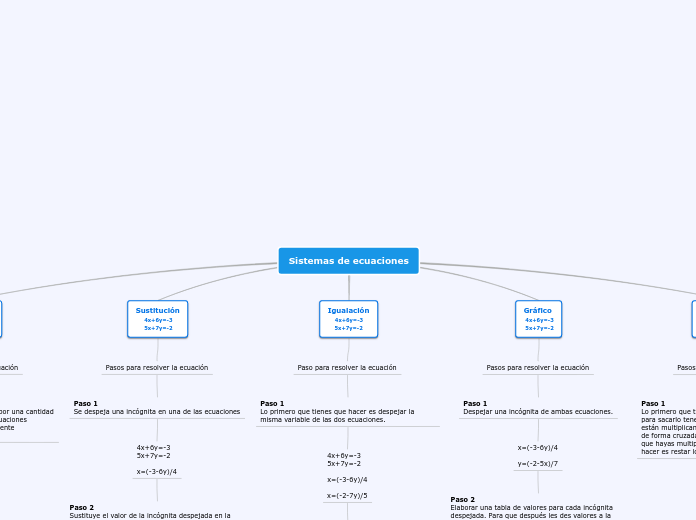
Sistemas de ecuaciones

Determinantes 4x+6y=-3 5x+7y=-2

Paso 1 Lo primero que tenemos que hacer es sacar delta; para sacarlo tenemos que multiplicar los valores que están multiplicando a "x" y "y" de ambas ecuaciones de forma cruzada, respetando signos. Después de que hayas multiplicado los valores, lo que tienes que hacer es restar los resultados.

4x+6y=-3 5x+7y=-2 6 x 5 4 x 7

30-28=2 Delta=2

Paso 2 Sacar delta "x", para eso tienes que multiplicar de forma cruzada respetando signo, los valores que están a la derecha del signo igual, y los valores que están multiplicando a la Y. Al sacar el resultado de las multiplicaciones restar los resultados.

4x+6y=-3 5x+7y=-2 -2 x 6 -3 x 7

-12-(-21) -12+21=9 Delta"x"=9

Paso 3 Sacar delta "y", para eso tienes multiplicar los valores que están a la derecha del signo igual, y los valores que están multiplicando a la X, de forma cruzada respetando signos. Al sacar el resultado de las multiplicaciones restar los resultados.

4x+6y=-3 5x+7y=-2 -3 x 5 -2 x 4

-15-(-8) -15+8=-7 Delta"y"=-7

Paso 4 Ahora que tenemos los valores de los determinantes (deltas), lo que sigue es encontrar los valores correspondientes a "x" e "y", y de esa forma resolvemos la ecuación. Para sacar el valor de "x" tienes que dividir delta"x" con delta, y para sacar "y" tienes que dividir delta"y" con delta.

x= 9/2 y=-7/2

Gráfico 4x+6y=-3 5x+7y=-2

Paso 1 Despejar una incógnita de ambas ecuaciones.

x=(-3-6y)/4 y=(-2-5x)/7

Paso 2 Elaborar una tabla de valores para cada incógnita despejada. Para que después les des valores a la incógnita que no esta despejada, para sacar las coordenadas y poder trazar una recta en un plano cartesiano.

Tabla de valores de la primera ecuación X Y -9/4 1 -3/4 0 9/4 -2 9/2 -7/2

Tabla de valores de la primera ecuación X Y 1 -1 0 -2/7 -1 3/7 9/2 -7/2

Paso 3 Teniendo las coordenadas podemos tazar nuestras rectas y el resultado será el punto (coordenadas) de intersección de las dos rectas.

Igualación 4x+6y=-3 5x+7y=-2

Paso para resolver la ecuación

Paso 1 Lo primero que tienes que hacer es despejar la misma variable de las dos ecuaciones.

4x+6y=-3 5x+7y=-2 x=(-3-6y)/4 x=(-2-7y)/5

Paso 2 Ya que despejaste las variables, lo que tienes que hacer es igualar las expresiones obtenidas y resolver la ecuación lineal.

(-3-6y)/4=(-2-7y)/5 5(-3-6y)=4(-2-7y) -15-30y=-8-28y -30y+28y=-8+15 -2y=7 y=-7/2

Paso 3 Con la ecuación ya resuelta, sustituimos el valor obtenido en cualquier ecuación del principio que tiene la incógnita despejada.

x=(-3-6y)/4 x=(-2-7y)/5 x=[-3-6(-7/2)]/4 x=(-3+21)/4 x=18/4 x=9/2

Sustitución 4x+6y=-3 5x+7y=-2

Paso 1 Se despeja una incógnita en una de las ecuaciones

4x+6y=-3 5x+7y=-2 x=(-3-6y)/4

Paso 2 Sustituye el valor de la incógnita despejada en la otra ecuación, como resultado tendrás una ecuación con una sola incógnita.

5x+7y=-2 5[(-3-6y)/4]+7y=-2

Paso 3 Ya que hayas sustituido, comienza a resolver la ecuación. Acuérdate que si hay denominador multiplicar toda la ecuación por el denominador.

4{5[(-3-6y)/4]+7y=-2} -15-30y+28y=-8 -2y=-8+15 -2y=7 y=-7/2

Paso 4 El valor obtenido de la ecuación anterior se sustituye en la ecuación en la incógnita fue despejada

x=(-3-6y)/4 x=[-3-6(-7/2)]/4 x=(-3+21)/4 x=18/4 x=9/2

Suma y resta 4x+6y=-3 5x+7y=-2

Pasos para resolver la ecuación

Paso 1 Multiplicar una o las dos ecuaciones por una cantidad constante adecuada para obtener ecuaciones equivalentes que tengan igual coeficiente (incógnitas) en común.

4x+6y=-3 5x+7y=-2 5(4x+6y=-3) 4(5x+7y=-2) 20x+30y=-15 20x+28y=-8

Paso 2 Por suma o resta (dependiendo de los signos de los coeficientes) se elimina una de las incógnitas.

4x+6y=-3 5x+7y=-2 5(4x+6y=-3) 4(5x+7y=-2) 20x+30y=-15 20x+28y=-8 (Resta)2y=-7

Paso 3 Resuelve la ecuación lineal resultante.

4x+6y=-3 5x+7y=-2 5(4x+6y=-3) 4(5x+7y=-2) 20x+30y=-15 20x+28y=-8 (Resta)2y=-7 y=-7/2

Paso 4 Ya que tengas el valor de la incógnita que resolviste sustitúyelo en cualquiera de las ecuaciones originales para, encontrar el valor de la otra incógnita.

4x+6(-7/2)=-3

Paso 5 Ya que hayas sustituido el valor de la incógnita, resuelve la ecuación.

4x+6(-7/2)=-3 4x-21=-3 4x=-3+21 4x=18 x=18/4 x=9/2