Vectores en R2 y R3

もっと見る

PROPIEDADES DE LA MULTIPLICACIÓN

SONIA YANETH FAJARDO OROZCOにより

Materia dispersa

A Fidalgoにより

Unidad 1. Habilidades Directivas y su Conceptualización.

Roberto Gaxiolaにより

Gas Natural

Génesis Cardozoにより

Vectores en R2 y R3

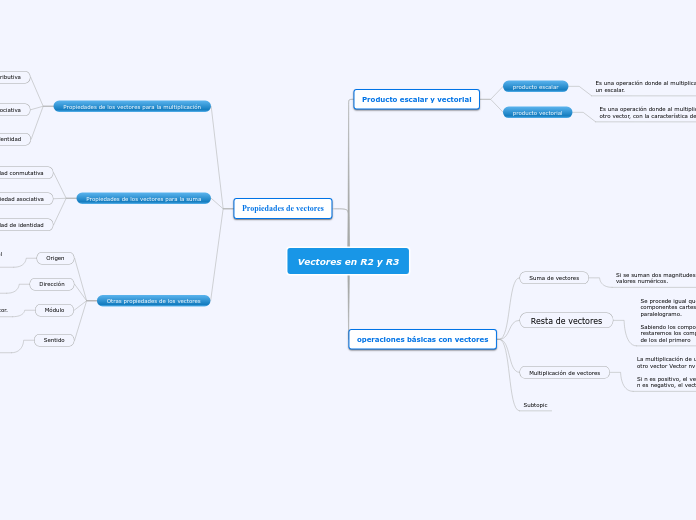
Propiedades de vectores

Otras propiedades de los vectores

Sentido

Este llega a indicar a través de una punta de flecha que se coloca en el extremo del vector, la dirección hacia donde el vector se dirige con relación a la línea de acción.

Módulo

Representa el tamaño o la longitud del vector.

Dirección

Representa la orientación en el espacio de la recta que lo posee.

Origen

También se le conoce como punto de aplicación. Se trata del punto con exactitud en donde el vector llega a actuar.

Propiedades de los vectores para la suma

Indica que hay un vector que llega a funcionar como un elemento neutro

Establece que no importa la forma en que se agrupen los vectores a la hora de sumar.

Propiedad conmutativa

Indica que no importa el orden en que los vectores se sumen su resultado es el mismo

Propiedades de los vectores para la multiplicación

Propiedad de identidad

Establece que el resultado al multiplicar un vector u por 1 siempre dará el mismo vector u.

Propiedad asociativa

Indica que el resultado al multiplicar los vectores c y d por el vector u, siempre será igual que la multiplicación del vector c por el producto entre el vector d y u.

Propiedad distributiva

Este establece que el resultado al multiplicar un vector independiente con otro que esté entre paréntesis es lo mismo que multiplicarlo ambos juntos.

operaciones básicas con vectores

Subtopic

Multiplicación de vectores

La multiplicación de un vector Vector v por un escalar n es otro vector Vector nv cuyo módulo será |n| · |Vector v|. Si n es positivo, el vector producto tendrá el mismo sentido. Si n es negativo, el vector producto tendrá el sentido opuesto.

Resta de vectores

Se procede igual que en la suma, bien operando con las componentes cartesianas, o bien mediante el método del paralelogramo. Sabiendo los componentes cartesianos de los vectores, restaremos los componentes cartesianos del segundo vector de los del primero

Suma de vectores

Si se suman dos magnitudes escalares, basta con sumar sus valores numéricos.

Producto escalar y vectorial

producto vectorial

Es una operación donde al multiplicar dos vectores se obtiene otro vector, con la característica de ser perpendicular a ambos.

producto escalar

Es una operación donde al multiplicar dos vectores se obtiene un escalar.