by mariana yermanos 4 years ago
302
More like this
divide todos los términos por el factor común y escribe el resultado entre paréntesis
el factor común es el producto de los terminos obtenidos 1 y 2
identifica las variables que aparecen en todos los terminos, escribe la variable con el menor exponente
identificar el máximo común divisor de los coeficientes de todos los terminos de la expresión
el residuo se obtiene multiplicando el coeficiente del ultimo termino del cociente por el segundo termino del divisor cambiado de signo y sumando este producto con el término independiente del dividendo.
el coeficiente de un termino cualquiera del cociente se obtiene multiplicando el coeficiente del termino anterior por el segundo termino del binomio divisor cambiando de signo y sumando este producto con el coeficiente del termino que ocupa el mismo lugar en el dividendo.
el coeficiente del primer termino del cociente es igual al coeficiente del primer termino del dividendo
el cociente es un polinomio en x cuyo grado es 1 menos que el grado del dividendo
se divide el prime termino del segundo resto entre el primero del divisor y se efectúan las operaciones anteriores. y así sucesivamente.
este segundo termino del cociente se multiplica por todo el divisor y el producto se resta del dividendo
se divide el primer termino del resto entre el primer termino del divisor y tendremos el segundo termino del cociente
este primer termino del cociente se multiplica por todo el divisor y el producto se resta del dividendo
se divide el primer termino del dividendo entre el primero del divisor y obtendremos el primer termino del cociente
se ordenan el dividendo y el divisor con relación a una misma letra
se multiplica todos los terminos del muultiplicando por cada uno de los terminos del muliplicador y se edusen los terminos semejantes
30x^3+10x+48x^2y+16y
(5x+8y)(6x^2+2)
se multiplica el monomio por cada uno de los términos del polinomio, teniendo en cuenta la regla de los signos.
10a^5+16a^2b
2a^2(5a^3+8b)
se multiplican los coeficientes y a continuación de este producto se escriben las letras de los factores en orden alfabetico, asinandole a cada letra el mismo exponente a la suma de los exponentes que tenga en los factores
=6a^5
2a^2 * 3a^3
Procedimiento
(Identificar y operar los términos semejantes de la expresión) 2w-5y-5x+3y-10w = -8w-2y-5x
(Aplicar ley de los signos, o cambiar el signo de cada término de la segunda expresión) (2w-5y)-(5x-3y+10w) =2w-5y-5x+3y-10w
(Ordenar)= (2w-5y)-(5x-3y+10)
(Enunciado) Restar (5x-3y+10w) de (2w-5y)
2. Una vez ordenada la resta, y haber realizado la ley de los signos con el negativo (-1) con cada uno de los términos de la segunda expresión; identificar y operar los términos semejantes.
2w-5y-5x+3y-10w
=-8w-2y-5x
1. Operar (multiplicar) cada término de la segunda expresión de la resta con el negativo (-1) previo, (o cambiar el signo de cada término de la segunda expresión).
De esta forma
(2w-5y)-(5x-3y+10w)
=2w-5y-5x+3y-10w
Para eso tener en cuenta la ley de los signos
-a*-a=a
a*-a=-a
a*a=a
En una frase tener en cuenta la palabra "de" para ordenar la resta.
de x reste y, es diferente a, reste x de y
(x-y) diferente a (y-x)
procedimiento
(5X+3Y)+(4X-4Y+Z)+(-3X+5Y+2Z)
(5X+4X-3X)+(3Y-4Y+5Y)+(Z+2Z)
=6X+4Y+3Z
2: sumamos los valores a los que se multiplica la variable (si no tiene numero previo a la variable en un termino, el numero al que la variable se multiplica es 1), solo operando los números y no las variables con sus respectivos exponentes (solo se operan entre si los términos semejantes, sin importar sus signos)
(3X^4)+(7X^4)
=10x^4
1: Identificar los términos similares, (es más simple si cada término semejante se subraya con un color)
Los términos semejantes son los que tienen la misma variable y exponente
(5Y^2)+(2X)
No son términos semejantes
(3X^4)-(7X^4)
Son términos semejantes
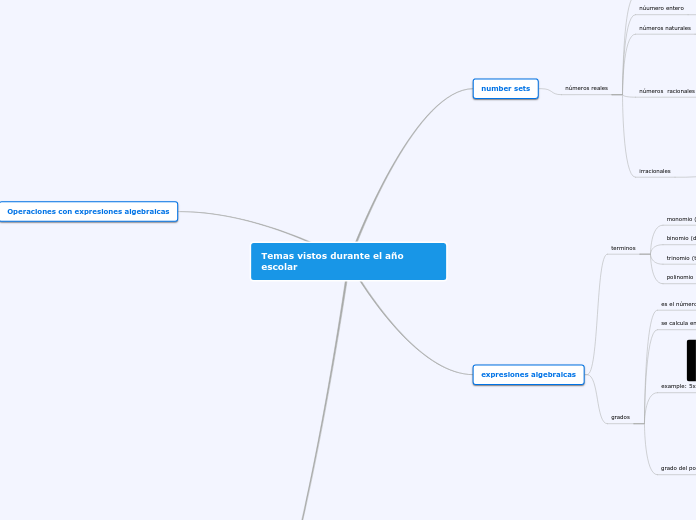
sexto o mas
sexto grado o x grado
quinto grado
quinto
cuarto grado
cuartico
tercer grado
cubico
^
segundo grado
cuadratica
1x^2+ 5x
primer grado
lineal
8x
no variable
constante
9
25+d^8-k^4+ 451f
14+ 148h- s^51
J^8+65, 70- V^7
5, 15y, m^5
como identificarlo?
sus números decimales son infinitos y ninguno se repite continuamente
1634.539654...
no se puede escribir en fracción
(10/2,,2/3,0.5)
de decimales a fracción
paso #3
simplifica el resultado
18/25
paso #2
Multiplica el numerador y el denominador por un 1 seguido de ceros, donde el cantidad de ceros es equivalente a los espacios decimales que tiene el numero para cada decimal
72/100
paso #1
write down the decimals as a fraction
0.72/1
de fracciones a decimal
Subtopic
(1,2,3,4)
(0,1,2,3)
(...-2,-1,0,1,2...)
