by Rebeca Bazua 8 years ago
350
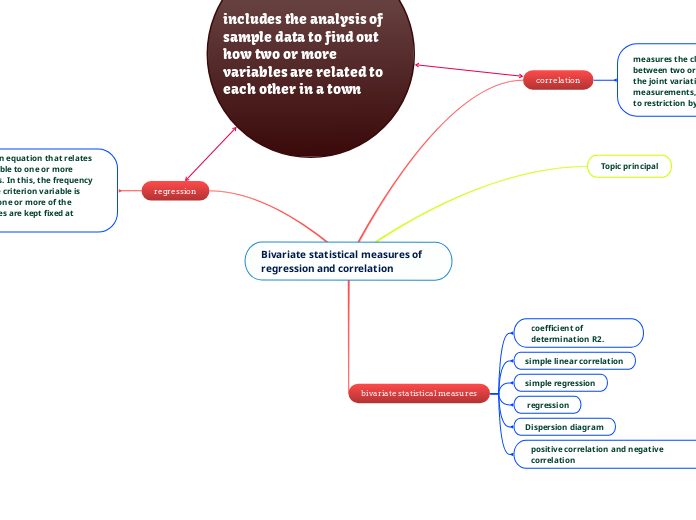
Increments and Differentials
Differentials and increments are mathematical concepts used to describe changes in quantities. Differentials provide an estimate of the change based on the tangent line of a function, symbolized as dy ≈ Δy and calculated using the derivative f'