MAT.126
3.5-3.6
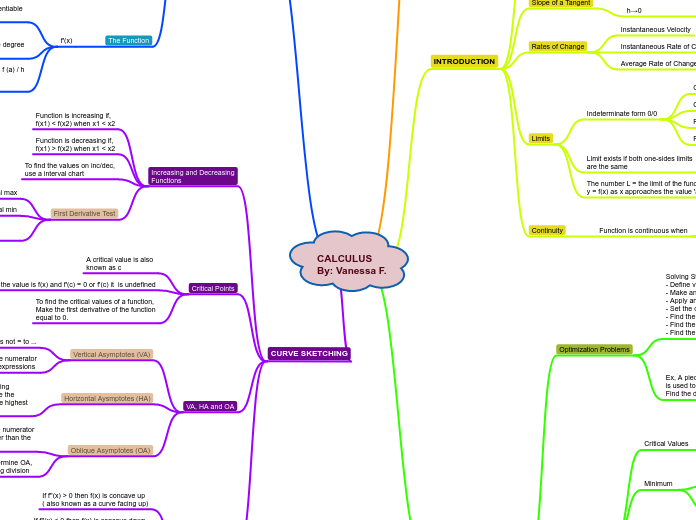
3.6 A Summary of Curve Sketching
Analyze and sketch the graph of a function
Polynomial Functions
In general, a polynomial function of degree n can have at most n - 1 relative extrema, and at most n - 2 points of inflection.
Polynomial functions of even degree must have at least on relative extremum.
Slant Asymptotes
The graph of a rational function (having no common factors and whose denominator is of degree 1 or greater) has a slant asymptote if the degree of the numerator exceeds the degree of the denominator by exactly 1.
To find the slant asymptote, use long division to rewrite the rational function as the sum of a first-degree polynomial and another rational function. The slant asymptote is the first-degree polynomial.
Guidelines
Determine the domain and range of the function.Determine the intercepts, asymptotes, and symmetry of the graph.Locate the x-values for which f'(x) and f''(x) are zero or do not exist. Use the results to determine relative extrema and points of inflection.Useful concepts
x-intercepts
y-intercepts
symmetry
domain
range
continuity
vertical asymptotes
differentiability
relative extrema
concavity
points of inflection
horizontal asymptotes
infinite limits at infinity
3.5 Limits at Infinity
Determine infinite limits at infinity
Let f be a function defined on the interval (a,infinity).
The statement lim(x-->infinity) = infinity means that for each positive number M, there is a corresponding number N > 0 such that f(x) > M whenever x > N.The statement lim(x-->infinity) = -infinity means that for each negative number M, there is a corresponding number N > 0 such that f(x) < M whenever x > N.Similar definitions can be written involving the cases where x-->-infinity.
Determine the horizontal asymptotes, if any, of the graph of a function
Functions can have different horizontal asymptotes to the right and the left
Guidelines for Rational Functions
If the degree of the numerator is less than the degree of the denominator, then the limit of the rational function is 0.If the degree of the numerator is equal to the degree of the denominator, then the limit of the rational function is the ratio of the leading coefficients.If the degree of the numerator is greater than the degree of the denominator, then the limit of the rational function does not exist. (When the degree of the numerator exceeds the degree of the denominator, a slant asympote exists.)Indeterminate Forms
0 / 0
infinity / infinity (also true if either infinity is negative)
Theorem 3.10
Limits at Infinity
If r is a rational number and c is any real number, then lim(x-->infinity) c / x^r = 0.
Furthermore, if x^r is defined when x < 0, then lim(x-->-infinity) c / x^r = 0.
Behavior
Functions can cross their horizontal asymptotes.
They cannot cross their vertical asymptotes.
The line y = L is a horizontal asymptote of the graph of f if lim(x-->-infinity) f(x) = L or lim(x-->infinity) f(x) = L.
Determine (finite) limits at infinity
Definition
Let L be a real number.
The statement lim(x-->infinity) f(x) = L means that for each epsilon > 0 there exists an M > 0 such that |f(x) - L| < epsilon whenever x > M.The statement lim(x-->-infinity) f(x) = L means that for each epsilon > 0 there exists an N < 0 such that |f(x) - L| < epsilon whenever x < N.
"End behavior"