Ley de los exponentes
Tipos de leyes
3a Ley: Producto de potencias con la misma base
Cuando dos potencias de la misma base, se multiplican, su resultado es un término de la
misma base y con un exponente igual a la suma de los exponentes de las potencias
multiplicadas.
6ta Ley: Potencia de un producto
La potencia de un producto es igual al producto de las potencias de los factores.
(a * b * c)n = an
* bn
* cn
Por ejemplo, al realizar la siguiente operación: (5*3)3, observamos que
(5*3)3 = (5*3)* (5*3) * (5*3) = (5*5*5) * (3*3*3) = 53
* 33
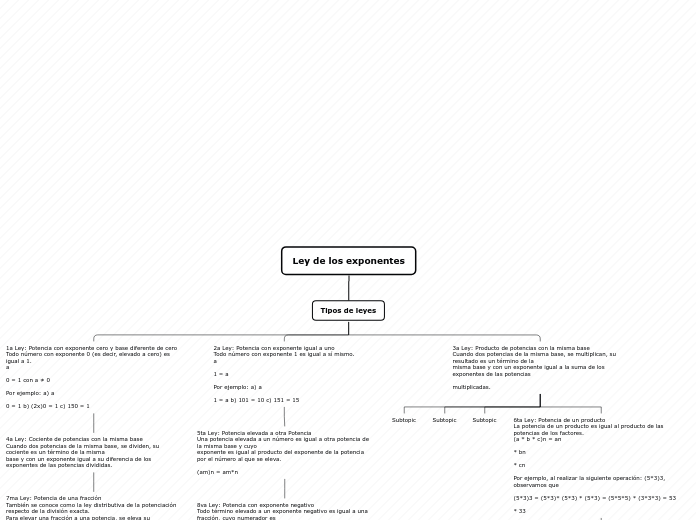
9na Ley: Potencia con exponente positivo
Todo término elevado a un exponente positivo es igual a una fracción, cuyo numerador es
la unidad y su denominador es el mismo término con el exponente negativo.
Subtopic
2a Ley: Potencia con exponente igual a uno
Todo número con exponente 1 es igual a sí mismo.
a
1 = a
Por ejemplo: a) a
1 = a b) 101 = 10 c) 151 = 15
5ta Ley: Potencia elevada a otra Potencia
Una potencia elevada a un número es igual a otra potencia de la misma base y cuyo
exponente es igual al producto del exponente de la potencia por el número al que se eleva.
(am)n = am*n
8va Ley: Potencia con exponente negativo
Todo término elevado a un exponente negativo es igual a una fracción, cuyo numerador es
la unidad y su denominador es el mismo término con el exponente positivo.
11va Ley: Exponentes fraccionarios
Provienen de extraer una raíz a una potencia cuando el exponente del término radicando
se divide por el índice de la raíz; si el cociente no es una cantidad entera, la división solo
queda indicada, dando lugar al exponente fraccionario.
1a Ley: Potencia con exponente cero y base diferente de cero
Todo número con exponente 0 (es decir, elevado a cero) es igual a 1.
a
0 = 1 con a ≠ 0
Por ejemplo: a) a
0 = 1 b) (2x)0 = 1 c) 150 = 1
4a Ley: Cociente de potencias con la misma base
Cuando dos potencias de la misma base, se dividen, su cociente es un término de la misma
base y con un exponente igual a su diferencia de los exponentes de las potencias divididas.
7ma Ley: Potencia de una fracción
También se conoce como la ley distributiva de la potenciación respecto de la división exacta.
Para elevar una fracción a una potencia, se eleva su numerador y su denominador a dicha
potencia
10ma Ley: Potencia negativa de una fracción
Si tenemos una fracción elevada a una potencia negativa, para quitar el exponente
negativo, invertimos la fracción.
