by luz dary florez 3 years ago
321
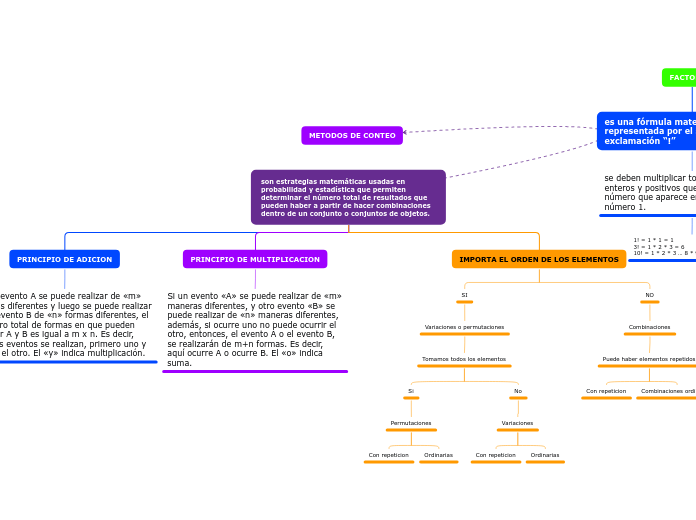
son estrategias matemáticas usadas en probabilidad y estadística que permiten determinar el número total de resultados que pueden haber a partir de hacer combinaciones dentro de un conjunto o conjuntos de objetos.
by luz dary florez 3 years ago
321

More like this
Puede haber elementos repetidos
Combinaciones ordinarias
Tomamos todos los elementos
No
Variaciones
Si
Permutaciones
Ordinarias
Con repeticion