door neftali diaz 5 jaren geleden
982
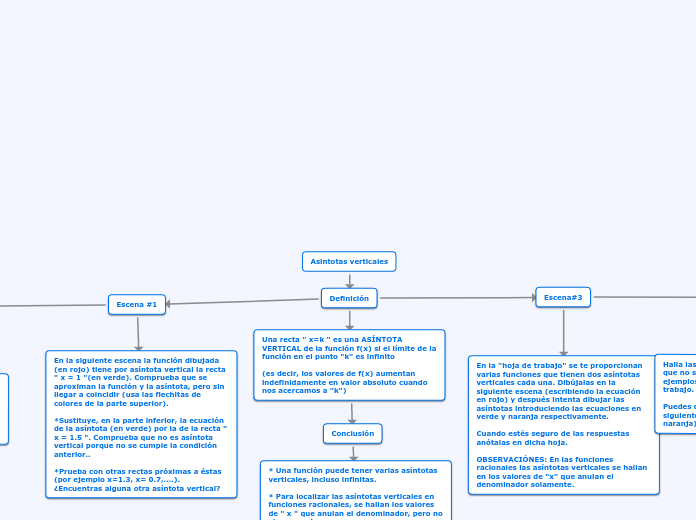
Asintotas verticales
Una asíntota vertical es una línea recta en la que el valor de una función racional se aproxima al infinito a medida que la variable independiente se acerca a un valor específico. Para identificar estas asíntotas, es necesario encontrar los valores que hacen que el denominador de la función sea cero, siempre y cuando el numerador no sea cero en esos puntos.