door Arthur Silva 4 jaren geleden
462
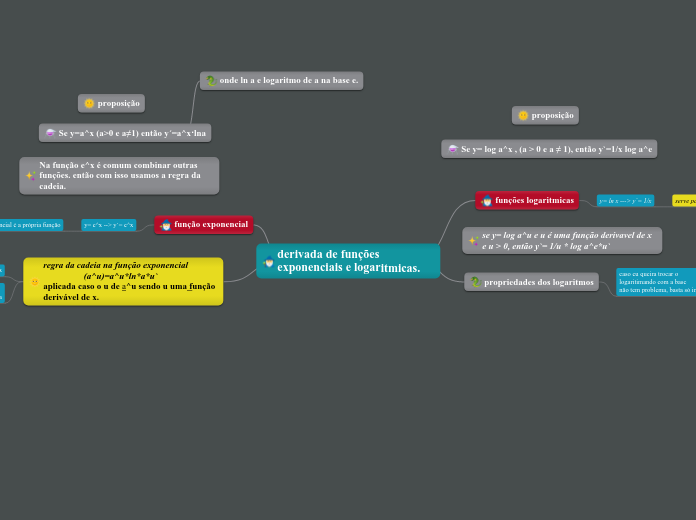
derivada de funções exponenciais e logaritmicas.
A derivação de funções exponenciais e logarítmicas é um tema central no cálculo diferencial, envolvendo frequentemente a aplicação da regra da cadeia. Para funções da forma y = a^x, onde a é uma constante positiva diferente de 1, a derivada resulta em y'