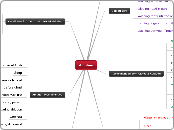
Is Your Differential Equation Linear?
Linear
Can It be put in the form:
y' + p(t)*y = f(t)?
Can the Variables be separated to all t on one side and y on the other?
ex: (2y)dy = (1/t)dt
Can the Equation be integrated Directly?
Try Checking The Non-Linear Side!
Integrate Directly!
Solve by separation of variables!
Use the integrating factor to solve.
Non-Linear
Were initial conditions given?
Example: y(0)=1, y'(0)=0
Does the function contain an exponential and can be placed in a similar order to:
y' = (r1 * x) + C*e^(r2*t) ?
Is it a second order differential equation equal to an exponent, constant or trig function?
Is it in the form of a matrix/system of equations?
Try Checking the Linear Side!
Solve using Eigen Vectors/Values
Solve using Undetermined Coefficients
Solve Using Variation of Parameters
Solve Using Laplace