Elementary Mathematics (Valentina Bitsoie)
Week Fourteen
Resources
Manipulative tools:
- number line
- cuisenaire rods
- fraction strips
- blocks
- base ten blocks
- interlocking linking cubes
- construction sets
- colored tiles
- pattern blocks
Resources
https://mathigon.org/polypad
https://nrich.maths.org/1249
https://play.google.com/store/apps/details?id=com.desmos.calculator&hl=en_US&gl=US&pli=1
https://www.mathway.com/Algebra
Fraction (Division):
Dividing Fractions:
Properties:
- Commutative property: the order of the numbers does not matter
ex) a/b=b/a, where a and b are rational numbers. a and b does not equal 0
ex) 12/3 does not equal 3/12
- Associative property: the operation can be applied regardless of how the numbers are grouped
ex) (a/b)/c=a/(b/c), where a, b, c are rational numbers, b and c can not equal 0
ex) (24/6)/2 does not equal 24/(6/2)
Property of division (same base):
a^m/a^n=a^m-n
Example:
(1/3)^11/(1/3)^4=(1/3)^6=1/3^6
Another Example:
(11/2)^3/(11/2)^3=(11/2)^0=1
Dividing fractions with models:
Example:

Area Models:
Rods:

Fractions (Multiplication):
Multiplying fractions:
Properties with the same bases
a^m*a^n=a^m+n
therefore,
property (a/b)^m=a^m/b^m
example:
(1/7)^3 *(1/7)^9= (1/7)^12= 1/7^12
Properties with different bases
example:
(2/3)^12*(4/9)^2
Find the LCM which, (4/9)= (2/3)^2
Rewrite equation: (2/3)^12*((2/3)^2)^3)
Simplify/Rewrite: (2/3)^12*(2/3)^6=(2/3)^18

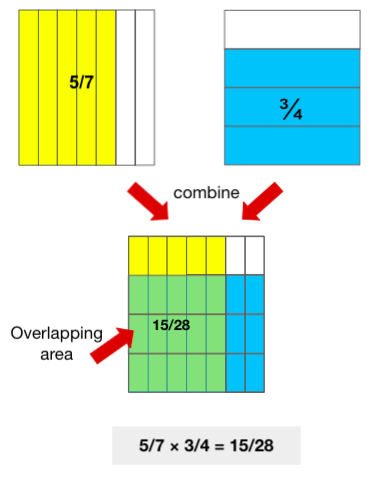
Multiplying using models/manipulative tools:
Area Model:
Pattern Blocks:

Objective: I will able able to... multiply and divide fractions with improper fraction, proper fractions, mental estimation and understand the properties.
Introduction: Rational Numbers (cont.)
Week Thirteen
Fractions(Subtraction)/HW/Resources (cont.)
Subtraction of Rational Numbers
if a/b and c/d are any rational numbers, then a/b-c/d is the unique rational number e/f such that a/b=c/d+e/f
Subtraction of rational numbers:
if a/b and c/d are any rational numbers, then
a/b-c/d=a/b+-c/d
If a/b and c/d are any rational numbers, then
a/b-c/d=ad-bc/bd
Finding each difference:
7/8-1/4=x
x=5/8
I was able to solve this using https://mathigon.org/polypad
without converting and was able find the difference without finding the LCM.
Fraction (Addition)
Various real number properties:
- Associative property
Example:

- Commutative property
Example:

- Identity Properties of Multiplication
Example:

Models:
Example of adding using fraction bars

Using pattern blocks:
example you could use the pattern block to add.

Definition of Addition of Rational Numbers with alike denominators
if a/b and c/d are rational numbers, then a/b+c/b=a+c/b
Definition of Addition of Rational Numbers with unlike denominators
if a/b and c/d are rational numbers, then a/b+c/b=ad+bc/bd
Example (denominators alike):
2/15+7/15=9/15
Example (denominators unlike):
4/14+5/7=?
Step 1) Find the LCM
which equals 14
Step 2) Convert the fraction into the LCM
so, 5/7=10/14
Step 3) Then add them together
so, 4/14+10/14=14/14=1
Objective: I will be able to... add and subtract fraction with same and different denominators. Moreover, I will be able to contexts, representations, various properties, mental computation, simplify, and to round.
Introduction: Cont. Rational Numbers
Week Twelve
Fraction & HW (resources)
- Equivalent Fraction Models:
Area Model of how equivalent fraction models

-Equivalent Fraction Models:
According to shows a whole that is divide into equal parts. Which could be a good visual for students to use to understand fractions.
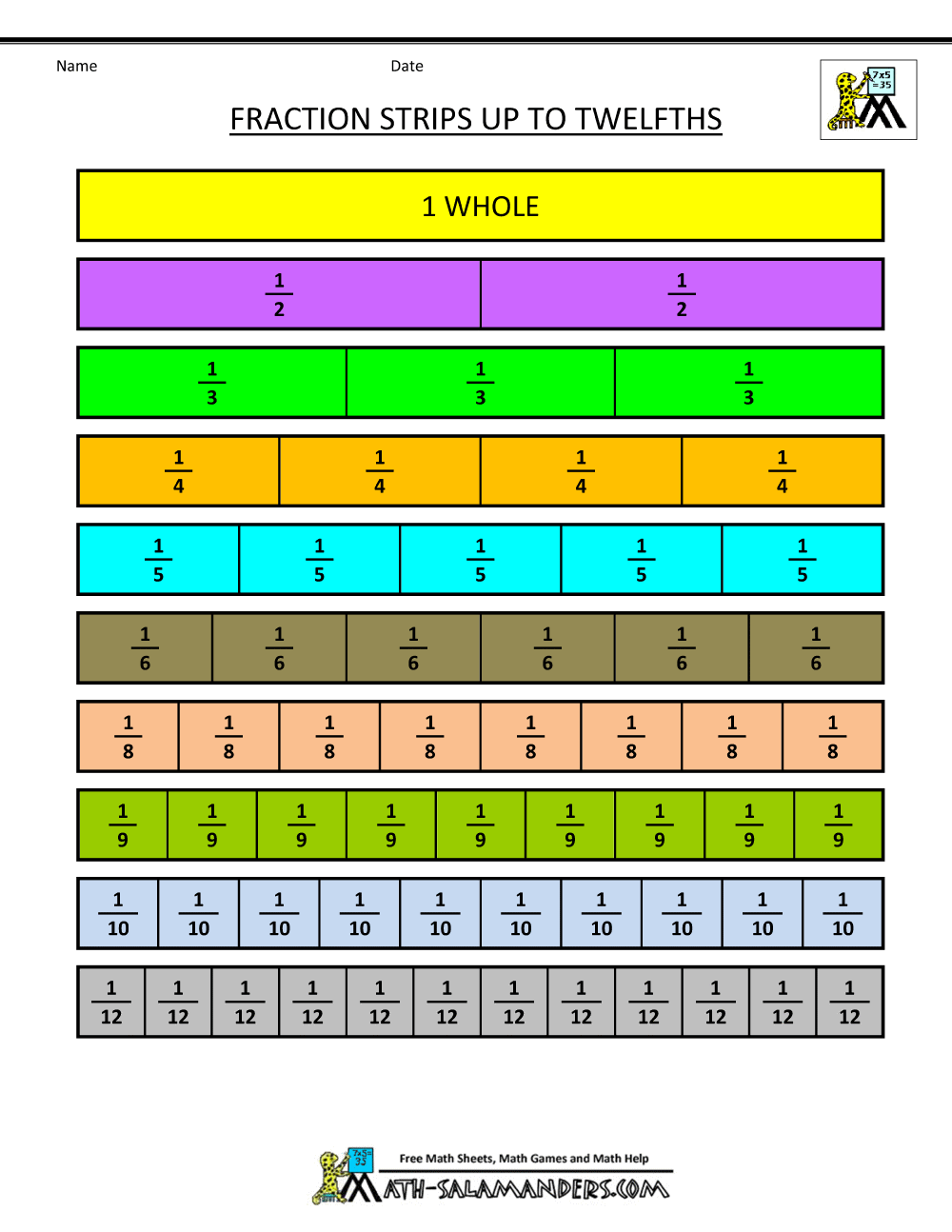
https://mathigon.org/polypad
Fraction
Introduction to Fraction: (Chapter 6-6.1)
Q={a/b where b cannot 0}
a as the numerator
b as the denominator
Example:
- Division/multiplication problem
- Portion/part/whole
- Ratio
- Probability
Illustration of fractions:
Bar model:

Number-line model:

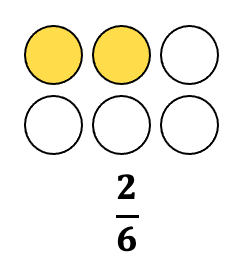
Set Model:

Fractions:
Two Types:
Proper fraction:
example:
4/7 is proper
Improper fraction:
example:
9/7 is improper
Fundamental Law of Fractions
If a/b is a fraction and n a non-zero number, then a/b=an/ba
Example: 2/-19=-2/19 because 2/-19=2(-1)/-19(-1)=-2/19
This is important when working with integers.
Simplifying fractions
Improper fraction (Mixed number):
24/3=8 or 26/3= 8 2/3
Proper Fraction:
2/12=1/6 or 12/24=12
Fractions can be converted to decimals as well.
Example:
2/5=2/5=0.4=40%
Objective: I will learn about rational numbers involving fractions and be able to addition and subtraction.
Introduction: Rational numbers
Week Ten
Percentage Change
Percent Change (Three Types of Problem)
- Increase: the amount has grown
example: 30 to 69
Percent change= 59-30
30
Percent change= 0.9666
Percent change= 96% (increase)
- Decrease: the amount has reduced
example: 39 to 25
Percent change= 39-25
25
Percent change=0.56
Percent change= 56%
Percent change= NEW AMOUNT- original amount
original amount
in-class example
Decimals (division/percentage)
Decimals and able to convert into percentage
0.26/2=0.13
Convert into percent= 13% is shaded
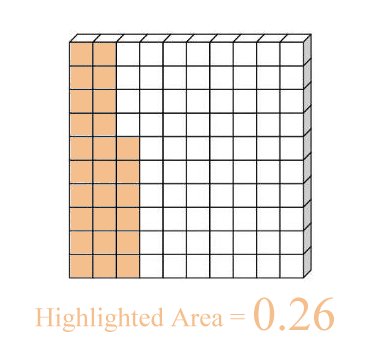
Find the percentage of the shaded circle:
Divide evenly by 20 by 100 which equals 5
therefore it is count the shaded area by 5 which equals 75 so that is 75% or 3/4 after to simplify.

Division of decimals using base ten:

https://www.mathsisfun.com/numbers/percentage-change.html
Objective: I will continue learning rational numbers, operations of decimals by being able to divide and convert into percentage.
Introduction: Rational numbers (Decimals and Fractions)
Week Nine
More resources for HW
https://www.google.com/search?client=firefox-b-1-d&q=online+calcultor
Decimals (multiplication) :)
Decimals, fraction, and percentage:
Example:
0.125 by 100%
0.125 × 100% = 12.5%
Answer 0.125 = 12.5%
Converting a decimal to percent: move the decimal two places to the right.
Example:
0.35 → 3.5 → 35%
Answer 0.35 = 35%

Another example:
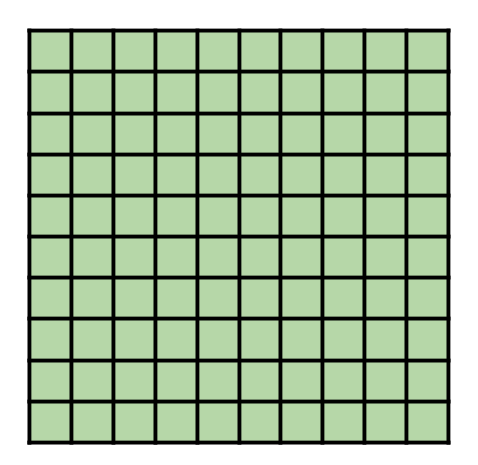
- 0.25 (a quarter) of the box is green.
- 25 of the 100 squares are green,
- 25 100 of the box is green,
- 25% of the box is green.
Objective: I will continue learning rational numbers and operations of decimals by being able to convert into a fraction and percentage.
Introduction: Rational Numbers Cont.
Week Eight
Multiplication (Base 10 blocks)
Multiplying decimals using base 10 blocks:
Example: 3 x 1.4 = 4.2



















Dividing decimals using base 10 blocks:
Example: 3.24/8=0.4
































Rational Numbers (decimals)
Objective: to compare and order decimals and to round numbers
Place Value:

Using base 10 blocks as place value:
Flat=1 Long=0.1 Cube=0.01


Example: 0.06






Desmos (a good resource)
able to use this as a classroom resource and visual.
Objective:I will learn rational number like operations, decimals of fractions, place value of decimals, comparison of decimal, using different algorithms, determining if a fraction will be termination or non-terminating decimals, and estimate.
Introduction: Rational Numbers
Week Seven
Irrational Numbers
Real (R): Any number found on the positive and negative number line
{...-3.4, …-1, … 0 …10, …, 2304.5…}
Integers (Z): Positive and negative whole numbers including 0
{..., -3, -2, -1, 0, 1, 2, 3…]
Rational (Q): Any number that can be expressed as fraction of two integers a & b
Irrational (P): Numbers that can not be written as a fraction of two integers, non-repeating decimals such as π (pi), Τ (tao), e
Natural (N): Counting numbers {1, 2, 3, 4, …}
imaginary (i): Square root of -1

Integers (division)
Division of real numbers:
- Inverse Property of Multiplication: every real number besides zero has a reciprocal and the product of any number is the reciprocal of one.
- Dividing by a number is the same as multiplying by its reciprocal
- Dividing by zero is impossible or no solution.
Rules:
Positive ÷ Positive =positive
Negative ÷ Negative = positive
Positive ÷ Negative = negative
Negative ÷ Positive = negative
Examples:
-56÷-7=8
Integers (multiplication)
Integers-multiplication rules
RULE 1: The product of a positive integer and a negative integer is negative.
RULE 2: The product of two positive integers is positive.
RULE 3: The product of two negative integers is positive.
Examples:
Rule 1: 1. (+4) x (-2) = -8 2. (-2) x (+5) = -10
Rule 2: 1. (+6) x (+8) = +48 2. (+6) x (+2) = +12
Rule 3: 1. (-6) x (-8) = +48 2. (-2) x (-4) = +8
Properties of multiplication:
Commutative Property of Multiplication: is the states that the answer remains the same when multiplying each numbers, changing the order will not change the product.
Example:
3x5=15
5x3=15
Associative Property of Multiplication: states that we multiply three numbers together, the product will be the same irrespective of the order in which we multiply the numbers.
Example:
2×(3×4)
2×(3×4)=2×12=24
Distributive Property of Multiplication: states that multiplication can be distributed over addition, as well as subtraction.
Example:
2×(3+1)
2×(3+1)=2×4=8
2×(3+1)=2×3+2×1=6+2=8
both cases, the answer we get is the same, hence, multiplication is distributive.
Identity Property of Multiplication: states that if you multiply any number by 1, the answer will always be the same number.
Example:
3×1=3
7×1=7
– If you multiply any number by 0, the answer will always be zero.
Integers using counters and chip model:
Example: 4x -2+-8

Objective: I will continue to explore and learn about integers such as mental computation, multiple algorithms, whole number representations, and counting. Then irrational numbers, real, numbers, and order of operations like relationship.
Introduction: Integers/Irrational Numbers
Week Six
Integers(adding/subtracting):
Negative integer= -n and are opposites of the positive integers.
Positive integer= +n and are opposites of the negative integers.
Absolute Value: for any integer x
lxl=x, if x > 0
lxl=-x, if x < 0
Example:
l20l= 20
l-20l= 20
Chip models: a yellow chip will represent a positive integer and a red chip will represent a negative integer.
Example:
https://www.basic-mathematics.com/modeling-integers.html
Using a number line: -3-4=-7

Types of Number:
Real (R): Any number found on the positive and negative number line
{...-3.4, …-1, … 0 …10, …, 2304.5…}
Integers (Z): Positive and negative whole numbers including 0
{..., -3, -2, -1, 0, 1, 2, 3…]
Rational (Q): Any number that can be expressed as fraction of two integers a & b
Irrational (P): Numbers that can not be written as a fraction of two integers, non-repeating decimals such as π (pi), Τ (tao), e
Natural (N): Counting numbers {1, 2, 3, 4, …}
imaginary (i): Square root of -1

Objective: I will understand integers operations like Basic operations on positive and negative numbers, use of properties, mental computation, multiple algorithms, whole number representations, and counting.
Introduction: Integers Operations
Week Five
LCM:
Least Common Multiple (LCM): as the smallest multiple that two or more numbers have in common.
Methods:
1) Colored Rods: is using the same manipulative tool of colored rods to compare the same length of blocks between the two numbers.
(Picture used from the slides)
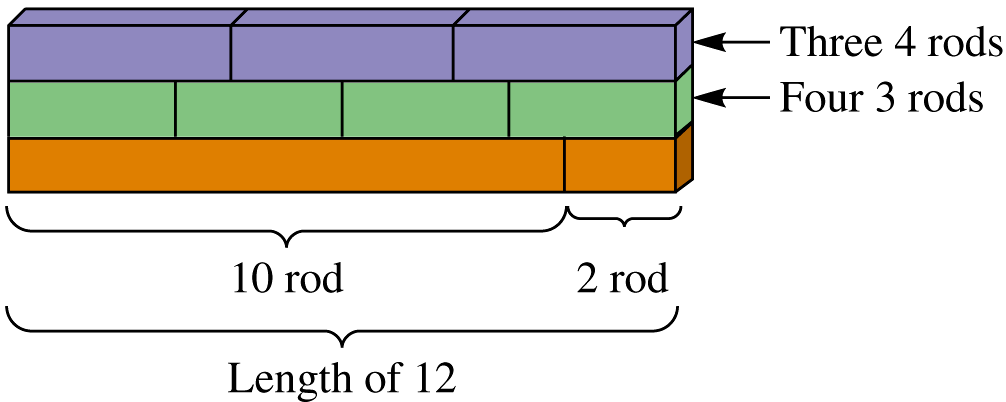
LCM (3,4)=12
2) Intersection of Sets: set of all multiples of each number and then intersect these sets to find the common multiples. The smallest element of the intersection is the least common multiple.
M6=6,12,18,24,30,36,42,48.54,60..
M8=8,16,24,32,40,48,56,64..
LCM(6,8)=24
3) Prime Factorization: find the prime factorization of both numbers. The LCM is the product of all of the primes in either number, raised to the greatest power that shows up in either prime factorization.
Example:
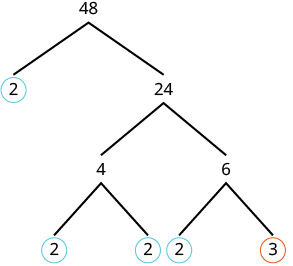
2⋅2⋅2⋅2⋅3
24⋅3= 48
4) Number Line: using a number line to find the where both numbers land on an exact point on the number line.
Example: LCM (3,4)= 12

5) Division by Primes: Divide the given numbers the least prime number
Example:

GCD/GCF:
Greatest Common Divisor (GCD)/Greatest Common Factor: is of two whole numbers known as a and b not both 0 is the greatest whole number that is divisible by both a and b.
Three Methods to finding GCD / GCF:
1) Colored Rods: is a manipulative tool such as the base 10 blocks, hands on by comparing two rods
Example:
Finding the Greatest Common Factor of Two Numbers The rods shown below show the factors of 6 and 8. Look at the rods and write down the factors of 6 and the factors of 8.
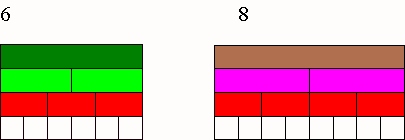
The 3 red rods build up to 6 but not 8
Then 4 red rods build up to 8 but not 6
Therefore the white rods are in 2 and build both so the GCD (6,8) =2
2) Prime Factorization Method: is the finding the GCD of two or more by identifying each common prime number. Then the product of common factors of it lowest prime factors together.
Example:

3) The Intersection of Sets Method: list all the member of whole number divisors of both numbers. Then pick the greatest element in that set.
Example:
Let set A = {2, 3, 4, 5, 6}
and set B = {3, 5, 7, 9}
In this two sets, the elements 3 and 5 are common
Divisibility:
Divisibility Rule:
2: must be even & must end in 0,2,4,6,8
3: sum must be divisible by 3
4: sum must divisible by four especially the last two digits
5: the last digit that end with 0 and 5 are divisible
6: the number must be divisible by 2 or 3
9: sum must divisible by 9
10: last digit with 0 are divisible
11: sum of the digits in odd-numbered places will equal to the sum of the digits in even numbered places or will differ
Although there are some special rules and could be divisible by different numbers
integer n is divisible by m if n=km
ex) 25 is divisible by 5
25=5x5
Objective: I will understand number theory by exploring the divisibility rules. Then explore examples and be able to find GCD/GCF and LCM.
Introduction: Number Theory
Week Four
Multiplication Algorithms/Methods
Multiplication Methods:
Method 1) Build up
This method is build up from what we know or considered mental math.
Ex. 12(11)
start with 12(10)= 120
then add 12 more which equal 132
Method 2) Multiplication with base 10 blocks
This method is using base ten blocks as a table.
https://www.coolmath4kids.com/manipulatives/base-ten-blocks
Method 3) Multiplication arrays
This is the creating array of numbers to visualize the product. Like,
https://quizizz.com/_media/quizzes/b7e8e498-427c-4f08-850b-81ef6ddbb233_900_900
Properties and Subtraction Algorithms
Subtraction Algorithms:
Expanded Form: 56-23=
56-20=36
36-3=33
Equal Addends: 524-158=
534+42=576
-158+42=-200
376
Problems in Different Bases:
53 bases 6 -14 base six=
algorithms: equal addends
53 six -14 six
53 six+ 2= 55 six
14 six +2= -20 six
35 six
Objective: I will learn the different properties, algorithms, and methods for subtraction and multiplication with manipulative blocks to understand different bases.
Introduction: Properties and algorithms of subtraction and multiplication.
Week Three
Standard Algorithm of Addition
The YouTube video helped me understand how to do standard algorithm of addition in different bases.
Standard Algorithm:
521
+371
892
Partial Sums:
435
+389
400+300=700
30+80=110
9+5=14
=824
Lattice Algorithm:
similar to expanded algorithm and uses diagonals to achieve regrouping.
Column Addition:
4 9 7
+ 3 6 5
7 15 12
8 5 12
862
Adding with bases and using different algorithm
35 base nine
+57 base nine
0 1
8 3
103 base nine
Order of operation
Order of operation: Solved from left to right whether its
1) Parenthesis ()
2) Exponents (9^2)
3) Multiplication/Division
4) Addition/Subtraction
Objective: I will learn and understand order of operation and different algorithms of addition to help solve linear equations with difference base system.
Introduction to order of operation, various algorithm of addition.
Week Two
Objective: I will and understand different bases and whole number operation.
Assignment of exploring different bases
Assignment introduced how to convert base ten into other various bases. For example 100 base six converted to base ten is 36.
Websites that helped me complete my assignment
Converting bases
used an online converter to check my work
Binary System
Introduction to bases, numeration systems, and whole number operation.
Week One
Class Session One/Two
Learned the difference of units
Explored different bases; such as unit(cube) is one, long (a line of cubes) is ten, and a flat (single big square) is hundred. Then explored how it would look in different bases.
History of One:
Discussion: What was surprising to you about the number systems? That discovery of one and zero made a big impact to numeral system, but to our future as well. Example: technology was created by pattern of one and zero.
Objective: I will learn the history and various numeral systems that will introduce the base and binary system.
Intro to MTE 280
Mindmap Overview with examples and rubric
Professor introduction, syllabus, expectation, and overview.