door Jazmin Quinones 3 jaren geleden
139
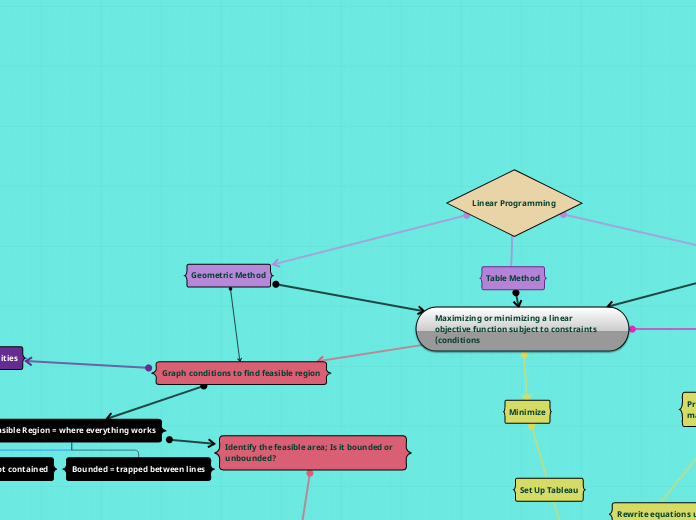
Geometric Method
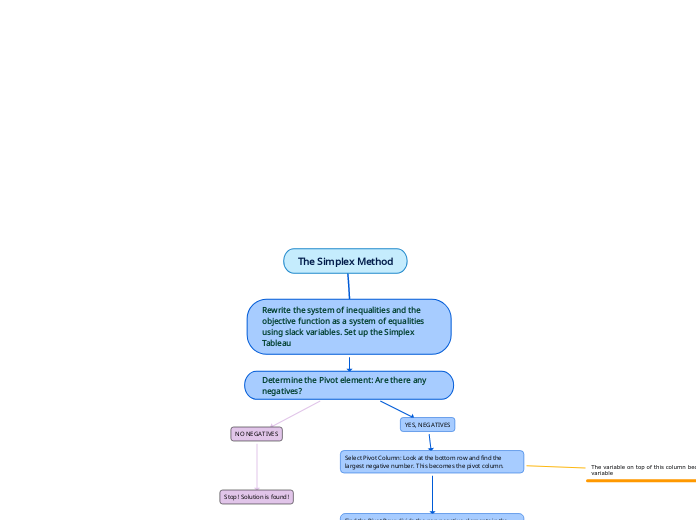
The simplex method is a mathematical approach used to solve linear programming problems by maximizing or minimizing a linear objective function subject to constraints. The process involves setting up a tableau, where rows and columns represent the equations and variables, respectively.