door Jorge Azul 3 jaren geleden
231
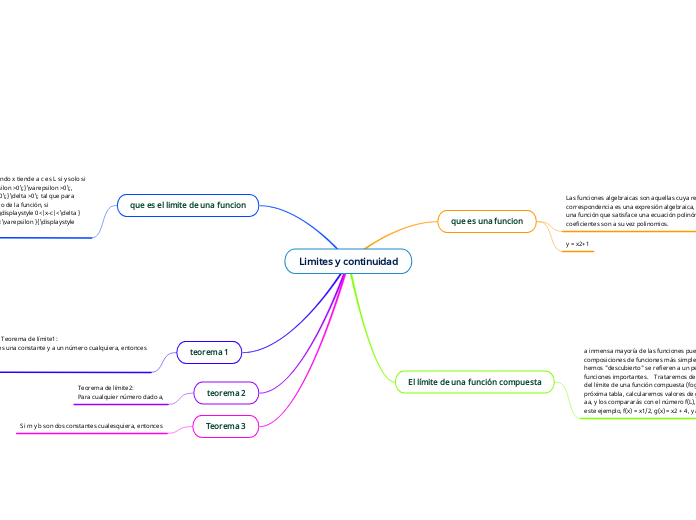
Limites y continuidad
La mayoría de las funciones pueden ser representadas como composiciones de funciones más simples, y los teoremas principales se enfocan en un grupo reducido pero significativo de estas funciones.