Linear Algebra Final

Meer zoals dit

VideoTerminals

door Pavel K

Vu Lam's math map

door Vũ Lâm

Retirement process changes

door Ian Caldwell

Out of Body Experiences

door Evan Bumgardner

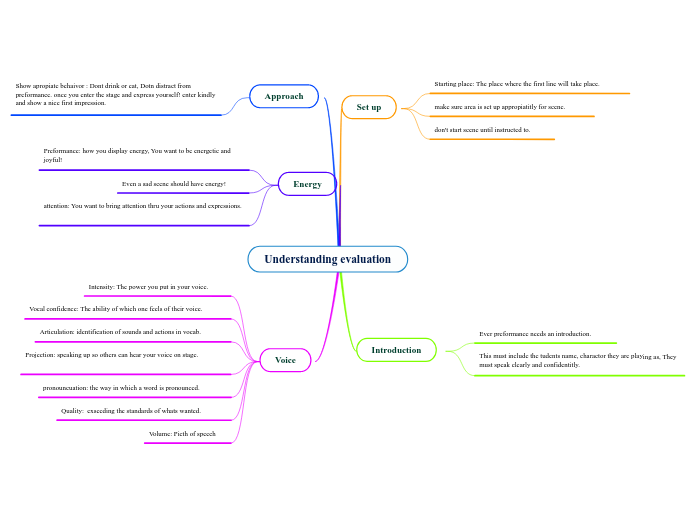
Millsaps College Linear Algebra Final Exam - Spring 2011 Textbook: Linear Algebra and Its Applications 3rd Edition by David C. Lay Instructor: Dr. Yan Wang

Test 4 (4.2 - 7!)

Orthagonality

Orthogonal Projection

The orthogonal decomposition theorem

Let W be a subspace of R^n. Then each y ∈R^n can be written uniquely in the form y = y-hat + z where y-hat ∈W and z ∈W⊥ In fact, if {u1,...,up} is any orthogonal basis of W, then y-hat = (y·u1/u1·u1)u1+(y·u2/u2·u2)u2+...+(y·up/up·up)up and z = y - y-hat

The vector y-hat ∈ the Orthogonal decomposition theorem is called the orthogonal projection of y onto W and often is written as proj_[w]_y

The length of z, ||z||, is the distance between y and the vector space W.

Given a nonzero vector u ∈ R^n, we can decompose any vector y in R^n as y = y-hat + z where y-hat=αu for some scalar α and z is some vector orthogonal to u. The vector y-hat is called the orthogonal projection of y onto u, and the vector z is called the component of y orthogonal to u.

it can be shown that y-hat = (y·u/u·u)u

Orthogonal Sets

An orthogonal basis for a subspace W of R^n is a basis for W that is also an orthogonal set

Let {u1,...,up} be an orthogonal basis for a subspace W of R^n. For each y in W, the weights in the linear combination y=c1u1+...+cpup are given by cj=y·uj/uj·uj

We can apply the Gram-Schmidt process to produce an orthogonal basis for any nonzero subspace or R^n

A set of vectors {u1,...,up} ∈ R^n is said to be an orthogonal set if each pair of distinct vectors from the set is orthogonal, that is, ui·uj=0 when i is not equal to j

Length, Distance, and Perpendicularity ∈ R^n

If a vector z is orthogonal to every vector in a subspace W of R^n, then z is said to be orthogonal to W. The set of all vectors z that are orthogonal to W is called the orthogonal complement of W and is denoted by W⊥

W=Span{[1,0]} W⊥=Span{[0,1]}

Two vectors are orthogonal to each other if

||u+v||^2=||u||^2+||v||^2

u·v=0

u^T * v

For u and v ∈ R^n, the distance between u and v, written as dist(u,v) is the length of the vector u-v. ||u-v||

Normalization

A vector whose length is 1 is called a unit vector. Given a vector v, the new vector u=v / ||v|| is a unit vector in the same direction as v

||av||=a||v||

The length or norm of v is the nonnegative scalar ||v|| defined by ||v||=sqrt(v·v) and ||v||^2 = v·v

Let u and v be vectors ∈ R^n with u=[u1,u2,...,un] and v=[v1,v2,...,vn]. Then the inner product (or DOT PRODUCT) of u and v, written u·v is u1v1+u2v2+...+unvn

u·v=(u^T)(v)

Symmetric Matrices

A symmetric matrix is a matrix such that A^T = A. Such a matrix is necessarily square

The Spectral Theorem for Symmetric Matrices

An nxn symmetric matrix has the following properties

A is orthogonally diagonalizable

The eigenspaces are mutually orthogonal

The dimension of the eigenspace for each eigenvalueλ equals the multiplicity of λ as a root of the characteristic equation

A has n real eigenvalues, counting multiplicities

A matrix A is said to be orthogonally diagonalizable if there are an othogonal matrix P (with P^-1 = P^T) and a Diagonalizable matrix D such that A = PDP^T=PDP^-1

An orthogonal matrix is a square matrix U such that U^-1 = U^T. Clearly the set of all column vectors from an orthogonal matrix forms an orthogonal set of unit vectors.

An nxn matrix A is orthogonally diagonalizable if and only if A isa symmetric matrix

If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal

Eigenvalues

Steps for Diagonalization (the eigen process)

Let A be an nxn matrix.

Find corresponding eigenvectors for eigenvalues of A by solving (A - λI)x=0

The dimension of the eigenspace is equal to the number of free variables in (A -λI)x=0

If the dimension of the eigenspace for each eigenvalue equals the multiplicity of that eigenvalue, then A is Diagonalizable

A=PDP^-1, where P is formed by the Eigenvectors and D is formed by the Eigenvalues corresponding the the eigenvectors

If the dimension of the eigenspace for each eigenvalue is not equal to the multiplicity of that eigenvalue, then A is NOT diagonalizable

All eigenvaectors and the zero vector from an eigenspace for each eigenvalue

Solve det(A - λI)=0 for λ to find all eigenvalues.

Check the algebraic multiplicity

Eigenvectors

Diagonalization Theorem

An nxn matrix is diagonalizable if and only if the sum of the dimensions of the distinct eigenspaces equals n, and this happens if and only if the dimension of the eigenspace for each eigenvalue equals the multiplicity of that eigenvalue

An nxn matrix with n distinct eigenvalues is diagonalizable

A=PDP^-1, with D a diagonal matrix, if and only if the columns of P are n Linearly independent eigenvectors of A. In this case, the diagonal entries of D are eigenvalues of A that correspond , respectively to the eigenvectors in P.

A square matrix is said to be diagonalizable if A is similar to a diagonal matrix, that is, if A=PDP^-1 for some invertible matrix P and some Diagonal matrix D.

An nxn matrix A is diagonalizable if and only if A has n Linearly independent eigenvectors.

If v1, ..., vr are eigenvectors that correspond to distinct eigenvalues λ1, ..., λr of an nxn matrix A, then the set {v1,...,vr} is linearly independent

Let λ be an eigenvalue of a square matrix A. Then the set consisting of the zero vector and all the eigenvectors corresponding to λ iscalled the eigenspace of A corresponding to λ. Note that the eigenspace of A corresponding to λ is Nul (A - λI)

If A is an nxn matrix, then det(A -λI) is a polynomial of degree n in λ, which is called the characteristic polynomial of A. The algebraic multiplicity of an eigenvalue λ is its multiplicity as a root of the characteristic equation.

The eigenvalues of a triangular matrix are the entries on its main diagonal

0 is an eigenvalue of a square matrix A if and only if A is not invertible

The scalar equation det(A - λI) = 0 is called the characteristic equation of A

A scalar λ is an eigenvalue of an nxn matrix A if and only if λ satisfies the characteristic equation det(A - λI)=0

λ is an eigenvalue of A if and only if the equation (A - λI)x=0 has a nontrivial solution

An eigenvalue of an nxn matrix A is a nonzero vector x such that Ax=λx for some scalar λ.. A scalar λ is called an eigenvalue of A if there is a nontrivial solution x of Ax=λx; such an x is called an eigenvector corresponding to λ

An eigenvector must be nonzero, but an eigenvalue may be zero

Dimension of a Vector Space

The Basis Theorem

Let V be a p-dimensional vector space, p at least 1. Any Linearly independent set of exactly p elements in V is automatically a basis for V. Any set of exactly p elements that spans V is automatically a basis for V.

If a vector space V has a basis of n vectors then every basis of V must consist of exactly n vectors

If a vector space V has a basis B = {b1, ..., bn}, then any set in V containing more than n vectors must be linearly dependent

Coordinate Systems

Suppose B={b1, ..., bn} is a basis for V and x is ∈ V. The coordinates of x relative to the basis B (or the B-coordinates of x) are the weights c1, ..., cn such that x=c1b1+...+cnbn. If c1,..., cn are the B-coordinates of x, then the vector in R^n [x]B = [c1,c2,...,cn] is the coordinate vector of x relative to B, or the B coordinate vector of x.

The mapping x |-> [x]B is the coordinate mapping (determined by B)

Let B = {b1, ..., bn} be a basis for a vector space V. Then the coordinate mapping x |-> [x]B is a one-to-one linear transformation from V onto R^n

The Unique Representation Theorem

Let B = {b1, ..., bn} be a basis for a vector space V. Then for each x ∈ V, there exists a unique set of scalars c1, ..., cn such that x=c1b1+...+cnbn

Basis

Let S be a basis for a vector space V. Then

S is also a Linearly independent set that is as large as possible because adding any vector to S results in a linearly dependent set

Span

S is a spanning set that is as small as possible because deleting any vector from S results in a non-spanning set of V

The pivot columns of A form a basis for Col A

Spanning Set Theorem

vp is a Linear combination of v1,v2,...,v(p-1) if [ v1 v2 ... v(p-1)] x = vp

Span {v1,...,vp}=Span{v1...v(p-1)}

Let S = {v1, ..., vp} be a set in V, and let H = Span {v1, ..., vp}

If one of the vectors in S--say vk--is a linear combination of the remaining vectors in S, then the set formed from S by removing vk still spans H

If H is not {0} (the null set), some subset of S is a basis for H.

Let H be a subspace of a vector space V. An indexed set of vectors B={b1, ..., bp} in V is a BASIS for H if:

the subspace spanned by B coincides with H

H = Span {b1, ..., bp}

B is a Linearly independent set

The range of T is the set of all vectors in W of the form T(x) for some x in V

The Kernel (or NULL SPACE) of a Linear transformation

the set of all u ∈ V such that T(u)=0.

A Linear Transformation T from a vector space V into a vector space W is a rule that assigns to each vector x in V a unique vector T(x) in W such that

T(cu)=cT(u) for all u ∈ V and scalars C

T(u+v) = T(u) + T(v) for all u,v ∈ V

Rank

Rank Theorem

Rank A + dimension Nul A = n

Let A be an mxn matrix. Rank A is equivalent to

Number of Basic Variables in A

The number of pivot positions in matrix A

The Dimension of Col A

Column Space

Col A is the set of all Linear combinations of the columns of A. If A = [a1 a2 ... an], then

dim Col A

number of basic variables in the matrix equation Ax=0

Col A = Span {a1, ..., an}

Null Space

Nul A is the set of all solutions to the homogenous equation Ax=0.

Dimension of Nul A

Number of Free Variables in the matrix equation Ax=0

Nul A = { x : x is ∈ R^n and Ax=0}

Subspace of R^n

The set of all solutions to a system Ax=0 of m homogenous Linear equations in n unknowns is a subspace of R^n

To check if a vector u is in the null space of A, simply solve the equation Au (not a matrix equation, but matrix A times a vector u). If the answer is 0, then u is in Nul A

Related to Eigenspace

Test 3 (2.5 - 4.1)

Vector Subspaces

A subspace of a vector space V is a subset H of V that has three properties

H is closed under multiplication by scalars.

for each u ∈ H and each scalar c, the vector cu is in H

H is closed under vector addition

for each u and v ∈ H, the sum u+v is in H

The zero vector of V is in H

Determinants

A and B are nxn matrices: det AB = (det A)(det B)

if A is an nxn matrix, then det A^T = det A

A square matrix A is invertible if and only if det A is not 0

A is a square matrix and B is the resultant matrix from one row operation

Scalar Multiplication

det(B) = k^(n) det A

interchange

det(B) = -det(A)

Replacement

det(B)=det(A)

Cofactor Expansion

Shortcut

If A is a triangular matrix, then det A is the product of the entries on its main diagonal

The determinant of an nxn matrix can be computed by cofactor expansion across any row or down any column

det A = a11C11+a12C12+...a1nC1n, where Cij = (-1)^(i+j) det Aij

LU Factorization

Row Reduce [L b] to find y.

Row Reduce [ U y ] to find x

Reduce A to an eschelon form U by a sequence of row replacements ONLY is possible.

Place entries in L such that the same sequence of row operations reduces L to I.

Test 2 (1.7 - 2.5)

inverse Matrix

The invertible Matrix Theorem

A Linear Transformation T : R^n -> R^n is said to be invertible if there exists a transformation S : R^n -> R^n such that S(T(x))=x for all x in R^n AND T(S(x))=x for all x in R^n

Let T : R^n -> R^n be a Linear transformation and let A be the standard matrix for T. Then T is invertible if and only if A is an invertible matrix. In that case, the linear transformation S given by S(x)=(A^-1)x is the unique function satisfying the previous conditions

S is the inverse transformation of T, written T^-1

Let A and B be nxn matrices. If AB=I, then A and B are both invertible with A=B^-1 and B=A^-1

A is an invertible, NxN matrix

Let C and D be NxN Matrices

CA=I; AD=I

C=D

A is row equivalent to I

A^T is invertible

(A^-1)^T is its inverse

Columns of A form a Basis for R^n

Rank A = n

Nul A = {0}

dim Nul A = 0

Col A = R^n

dim Col A = n

For all B ∈ R^N, Ax=b has the unique solution x=(A^-1)b

x |-> AX is ONE-TO-ONE

The Columns of A are Linearly Independent

The columns of A do not contain the Zero Vector

det A is not 0

0 is NOT an eigenvalue of A

At Most One Solution

x |-> Ax maps R^N ONTO R^N

A has N pivot columns

The Columns of A Span R^N

b is a Linear combination of the columns of A

N Pivot Positions

At least ONE solution

Algorithm for finding A^-1

Row reduce the augmented matrix [ A I ]. If A is row equivalent to I, then [ A I ] is row equivalent to [ I A^-1]. Otherwise, A does not have an inverse.

The Product of invertible Matrices is Invertible and the inverse is the product of their inverses in the reverse order

(A^T)^-1 = (A^-1)^T

If A and B are nxn invertible matrices, then so is AB, and the inverse of AB is the product of the inverses of A and B in the reverse order. That is, (AB)^-1 = (B^-1)(A^-1)

If A is an invertible matrix, then A^-1 is invertible and (A^-1)^-1 = A

Theorem 4 (2.2)

If A is an invertible nxn matrix, then for each b in R^n, the equation Ax=b has the unique solution x = (A^-1)b

2x2 inverse

A^-1 = (1/ad-bc) [d -b, -c a]

ad-bc = det A, which is the Determinant of A

Let A = [a b, c d]. If ad-bc is not equal to 0, then A is invertible

An nxn matrix A is said to be invertible is there is an nxn matrix C such that CA=I and AC=I, where I is the nxn identity matrix. C=A^-1 (A inverse)

Non-singular Matrix

invertible Matrix

Singular Matrix

NOT invertible

Transpose Matrix

Properties

(AB)^T = (B^T)(A^T)

for any scalar r, (rA)^T = rA^T

(A+B)^T = A^T + B^T

(A^T)^T=A

The transpose of an mxn matrix is denoted A^T and changes A's rows for its columns

A is mxn, A^T is nxm

Matrix Operations

WARNINGS

If AB=0, you cannot conclude that A=0 or B=0

If B=C, AB is not always equal to AC

AB is not always equal to BA

IA=A=AI

r(AB)=r(A)B=A(rB) for any scalar r

(B+C)A=BA+CA

A(B+C)=AB+AC

A(BC)=(AB)C

Linear Transformation

The Matrix of a Linear Transformation

Assuming that T : R^n -> R^m is a linear transformation, there exists a unique matrix A, such that T(x)=Ax for all x in R^n

A is the mxn matrix whose jth column is the vector T(ej)

The Standard matrix for the Linear transformation T

A = [ T(e1) ... T(ej) ]

Identity Matrix

ej is the jth column of the identity matrix ∈ R^n for 1

has 1's on the diagonal and zeros elsewhere

nxn matrix denoted I

Existence and Uniqueness Questions

ONE-TO-ONE

The columns of a matrix A are Linearly independent

T(x)=0 has ONLY the trivial solution

A mapping T : R^n -> R^m is said to be one-to-one if each b in R^m is the image of at MOST one x in R^n

T(x1) is not equivalent to T(x2) when x1 is not equivalent to x2

ONTO

Columns of a matrix A span R^m

A mapping T : R^n -> R^m is said to be onto R^m if each b in R^m is the image of at LEAST one x in R^n

A transformation (or mapping) T is linear if:

All Matrix transformations are Linear transformations

T(0)=0

T(cu+dv)=cT(u)+dT(v) for all vectors u,v and scalars c,d

T(cu)=cT(v) for all u and scalars c

T(u+v)=T(u)+T(v) for all u,v ∈ the domain of T

A transformation (or function or mapping) T from R^n to R^m, denoted by T : R^n -> R^m, is a rule that assigns to each vector x in R^n a vector T(x) in R^m.

For x ∈ R^n, the vector T(x) in R^m is called the image of x (under the action of T). The set of all images T(x) is called the range of T

The set R^m

The CODOMAIN of T

The set R^n

DOMAIN of T

Linear Dependence

A set that contains more vectors than entries in each vector

A is an mxn matrix

n > m

S={v1, ..., vp}

Set contains the zero vector

there exists at least one vector in S that is a linear combination of the others

Set of TWO vectors

Scalar multiples

The set {v1, ..., vp} is said to be Linearly dependent if there exists weights c1, ..., cp not all zero, such that c1v1+c2v2+...+cpvp=0.

Linear Independence

{v1, ..., vp} does NOT contain the zero vector

Ax=0 has only the trivial solution

An indexed set of vectors {v1, ..., vp} in R^n is said to be linearly independent if the vector equation x1v1+x2v2+...+xpvp=0 has ONLY the trivial solution

Test 1 (1.1 - 1.6)

Theorem 5 (1.4)

About COEFFICIENT matrices

Let A be an mxn matrix. The following are logically equivalent

A has a pivot position in every row

The columns of A span R^m

Each b ∈ R^m is a linear combination of the columns of A

For each b ∈ R^m, the equation Ax=b has a solution

Existence and Uniqueness Theorem

A Linear system is consistent if and only if the rightmost column of the augmented matrix is NOT a pivot column--that is, if and only if an eschelon form of the augmented matrix had no row of the form [0 0 0 ... 0 b], with b nonzero

If a Linear system is consistent then the solution set contains either

infinitely many solutions

at least one free variable

a unique solution

no free variables

Definitions

Homogenous System

For a given equation Ax=0, a nontrivial solution is a nonzero vector x that satisfies Ax=0

Happens when there is at least one free variable

Parametric Vector Form

The zero solution of Ax=0 is called the trivial solution.

A Linear system is homogenous if it can be written in the form Ax=0, where A is an mxn matrix and 0 is the zero vector in R^m.

Span of Vectors

The collection of all vectors that can be written in the form c1v1+c2v2+...+cpvp with c1, ..., cp scalars

Linear Combination of Vectors

Given the vectors v1, v2, v3, ..., vp ∈ R^n and given scalars c1,c2, ..., cp in R, the vector y defined by y=c1v1+c2v2+...+cpvp is called a linear combination of v1, v2, ..., vp with weights c1, c2, ..., cp

Free Variable

Variable not corresponding to a pivot column

Basic Variable

Variable corresponding to a pivot column

Pivot Column

Column of A containing a pivot position

a location in A that corresponds to a leading 1 in the reduced echelon form of A

echelon Form

Reduced echelon Form

Unique Row Reduced Matrix for each Eschelon matrix

Each leading 1 is the only nonzero entry in its column

The leading entry of each nonzero row is one

each leading entry of a row is in a column to the right of the leading entry of the row above it

all entries in a column below a leading entry are zeros

All nonzero rows are above any rows of all zeros

Consistent Linear System

One or more solution